접미사 배열(Suffix Array)

접미사 배열(Suffix Array)

접미사 배열은 문자열 S의 모든 접미사를 사전순으로 정렬해 놓은 배열.

ex) S = "banana"에는 접미사가 총 6 개 있습니다.

      "banana", "anana", "nana", "ana", "na", "a"

▶Suffix[i] = [5, 3, 1, 0, 4, 2]

※ 문자열 매칭이나 압축 등과 같은 작업에 사용.

 

문자열 길이 N 이 너무 크지 않을 때, 접미사를 일일이 구한 다음 (O(N))

정렬 (O(N logN))하면 되기 때문에 시간복잡도: O(N2 × logN)

- [BOJ] 11656 접미사 배열 (단순히 접미사를 오름차순으로 정렬하는 문제)

[BOJ] 백준 11656 접미사 배열

 

Manber-Myers Algorithm

※ 접미사 배열을 O(N × log2N)으로 구할 수 있습니다.

    (+ O(N), O(N logN) 소요되는 알고리즘도 존재)

 

문자열의 크기를 1, 2, 4, 8 ... 2n 기준으로 정렬합니다. O (logN)

각 단계별로 정렬에 소요 시간 O(NlogN)이므로, 총 O(N × log2N) 소요

아래 예제는 "banana"의 문자열의 길이 = 6이기 때문에 여덟 글자 기준 정렬 X

 

Suffix Array 구현

※ Geeksforeeks 참고

① 각 접미사(Suffix)의 첫번째 글자를 기준으로 Rank 값 할당

for (int i = 0; i < N; i++) {
    // a:0, b:1, c:2, ..., z:25
    int rank = str.charAt(i) - 'a';
    sa[i] = new Suffix(i, rank);
}

　

② 두 번째 글자를 기준으로 Next Rank 값 할당

    (두번째 글자가 없는 경우 『-1』 할당)

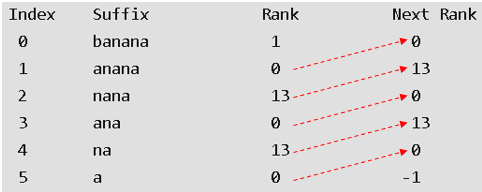
접미사 배열 순서상 다음 원소의 Rank가 현재 원소의 Next Rank입니다.

※ 마지막 원소는 한 글자이므로 『-1』 일 수밖에 없습니다.

// 접미사 앞에서 두번째 글자로 nextRank 계산
for (int i = 0; i < N-1; i++) {
    // 현재 접미사의 두번째 글자과 다음 접미사의 두번째 글자와 동일.
    sa[i].nextRank = sa[i+1].rank;
}
sa[N-1].nextRank = -1;

　

③ (1차 기준) Rank, (2차 기준) Next Rank으로 오름차순 정렬

Arrays.sort(sa);

...중략...

class Suffix implements Comparable<Suffix> {
     int index;
     int rank, nextRank;
     public Suffix(int index, int rank) {
           this.index = index;
           this.rank = rank;
     }
     public int compareTo(Suffix target) {
           // 같은 경우:0, 작은 경우: -1, 큰 경우: 1
           if (this.rank != target.rank)
                return Integer.compare(this.rank, target.rank);
           // rank가 동일하면 nextRank로 비교
           return Integer.compare(this.nextRank,  target.nextRank);
     }
}

▶ 첫번째, 두번째 글자를 기준으로 정렬완료

 

④ Rank 값 갱신

- 정렬된 첫번째 원소 Rank = 0 할당

- 이전 원소와 현재 원소의 (Rank, Next Rank) 값 비교

   : 같으면 이전 원소의 할당된 Rank값을 그대로 할당

   : 다르면 이전 원소의 할당된 Rank값 + 1

　

⑤ Next Rank 갱신 (4, 8, 16,,, 글자 기준)

※ [참고] Next Rank 갱신은 Rank 값을 이용해 갱신합니다.

현재는 4번째 글자를 기준으로 정렬해야 하기 때문에

a. 기존까지 확인한 글자 위치 + length(=4) / 2를 Index 값에 더해줍니다.

b-1. 더해준 값이 해당 Suffix 길이보다 크면 Next Rank = -1

b-1. 더해준 값이 Suffix 값 이하이면 해당 Index를 가지고 있는 Rank값을 Next Rank로 할당

(3, ana)의 경우

    ① (3, ana)에서 현재 인덱스 3 → 3 + (length/2) = 3 + 2 = 5

    ② index = 5인 (5, a)의 rank = 0을 (3, ana)의 Next Rank = 0으로 할당

(2, nana)의 경우

    ① (2, nana)에서 현재 인덱스 2 → 2 + (length/2) = 2 + 2 = 4

    ② index = 4인 (4, na)의 rank = 3을 (2, nana)의 Next Rank = 3으로 할당

★위의 과정을 (5, a), (1, anana), (3, ana), (0, banana), (2, nana), (4, na) 차례대로 수행하며,

    ①에서 도출한 Index 값 ②의 Index를 쉽게 mapping 하기 위해 temp[] 배열 사용 

 

⑥ 갱신된 Rank와 Next Rank로 재정렬

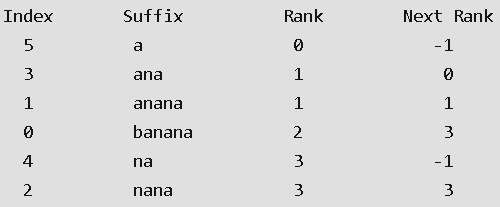
▶ ④. ⑤, ⑥ 작업을 4, 8, 16, ..., 2n 으로해서 2n <  까지 반복.

 

※ LCP (Longest Common Prefix) 참고

 

LCP (Longest Common Prefix)

 

Reference

- [BOJ] 11656 접미사 배열 

- [BOJ] 9248 Suffix Array 

- [BOJ] 1605 반복 부분문자열