반응형
기수 정렬
- O(N + K)
- 원소들의 자릿수에 따라서 정렬
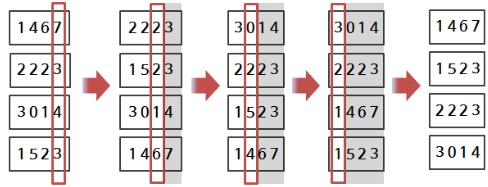
① 1의 자릿수를 기준으로 정렬
② 10의 자릿수를 기준으로 정렬
③ 100의 자릿수를 기준으로 정렬
④ ... 최대 자릿수의 길이만큼 반복
작은 자리수부터 비교하는 방식을 LSD
큰 자리수부터 비교하는 방식을 MSD
시간복잡도는 O(N + K)로, K는 최대 자릿수의 길이.
구현
일반적으로는 각 자릿수 오름차순으로 담기위해 Queue를 이용합니다.
① 1의 자릿수를 기준으로 정렬
- 자릿수에 따른 큐에 원소를 집어넣는다. (N번)
- 큐에 있는 원소를 pop() 하여 원소를 재배열 합니다. (N번)

② 10의 자릿수를 기준으로 정렬

③ 100의 자릿수를 기준으로 정렬

- 최대 자릿수의 길이 = 3이므로 총 3번 진행
- (십진수의 경우) 0~9까지의 자릿수를 담으므로 10개의 Queue 이용.
이진수나 문자열과 같이 큐의 개수가 변할 수 있음
ex. [“orange”, “harbang”]
- 부동소숫점이 없는 정수여야 한다 (ex. [2.14, 17.1] 와 같은 리스트는 정렬 불가)
+ 버킷(Queue)과 같은 추가 메모리가 필요한 단점 존재.
Code
#include <iostream>
#include <queue>
using namespace std;
void radixSort(int arr[], int n) {
// 최대 자리수를 가진 숫자를 구합니다.
int max = arr[0];
for (int i = 1; i < n; i++) {
max = max > arr[i] ? max : arr[i];
}
// 최대 자리수를 구해낸다.
int k = 1;
while (max / 10) {
k *= 10;
max /= 10;
}
queue<int> queue[10];
int digit = 1, mod = 10;
while (digit <= k) {
// 자리수에 맞게 Queue push
for (int i = 0; i < n; i++) {
queue[(arr[i] % mod) / digit].push(arr[i]);
}
// Queue에 들어가 있는 원소를 배열에 재배치
int j = 0;
for (int i = 0; i < 10; i++) {
while (queue[i].size() > 0) {
arr[j++] = queue[i].front();
queue[i].pop();
}
}
// 비교할 자릿수 변경
digit *= 10; mod *= 10;
}
}
void main(void) {
int n = 8;
int arr[8] = { 170, 45, 75, 90, 2, 24, 802, 66 };
radixSort(arr, n);
for (int i = 0; i < n; i++) {
cout << arr[i] << ' ';
}
}

반응형
'알고리즘' 카테고리의 다른 글
| DFS와 BFS 비교 (0) | 2021.02.24 |
|---|---|
| [예제] 합병 정렬 (Merge Sort) (0) | 2021.02.23 |
| 정렬 알고리즘 비교 (0) | 2021.02.23 |
| 접미사 배열(Suffix Array) (0) | 2021.02.23 |
| 선택 정렬(Selection Sort) (2) | 2021.02.23 |





댓글