정렬 알고리즘 비교

시간 복잡도 비교

▶ O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!) < O(nⁿ)

 

 

정렬 알고리즘 시간 복잡도

 

 

특징

 

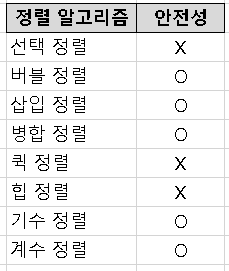
안전성은 주어진 배열 원소의 배치와 상관없이 구현 속도에 변함이 없는가를 의미합니다.

즉, Worst, Best, Average의 시간복잡도가 동일한 경루를 의미합니다.

- 힙 정렬은 추가 메모리 따로 필요없을 뿐더러, 주어진 배열의 원소 배치와 상관없이 O(N log N) 지님

- 병합정렬도 마찬가지로 O(N log N) 입니다.

- 퀵 정렬은 Pivot 변화에 따라서 시간 복잡도가 달라집니다.

   즉, 원소가 편향적으로 배치된 경우에는 최악의 시간복잡도가 생김 O(N2)

 

 

Q. 추가적인 메모리를 할당할 수 없을 경우, 데이터의 배치가 엉망일 수 있다면 적절한 알고리즘은?

A. 퀵 정렬

데이터의 배치가 불안정한 것에 퀵 < 병합이지만, 추가 메모리 확보가 안된다면 퀵을 선택해야 합니다.

 

 

Q. 배열 A[1...N]이 이미 정렬되어 있는 상태일 때, 가장 효율적인 알고리즘은?

A. 삽입 정렬 ← 선형시간

 

 

Reference

- [알고리즘] 시간 성능 향상을 위한 코드 최적화 (C/C++)  

- [알고리즘] 알고리즘 문제에서 시간 복잡도는 어떻게 하는걸까?

- [알고리즘] 코딩 테스트 문제 풀 때, 시간 복잡도 계산해보기

- [C/C++] time(), clock()으로 실행시간 측정  

- [ps] 문자열 사전 오름차순 비교 및 정렬  

- [ps] 여러 정수 기준에 따른 우선순위 비교 및 정렬