연속된 부분 합(연속합) - 1 (완전 탐색)

※ 구간합을 구하는 효율적인 방법

연속된 부분 합(연속합) - 1 (완전 탐색) 

연속된 부분 합(연속합) - 2 (Prefix Sum)

연속된 부분 합(연속합) - 3 (DP)  

[구간합] Sum of sub-matrix (2D Array) 

완전 탐색

Q) 아래와 같이 배열이 주어질 때 특정 연속 구간의 합 중 최대값을 구하시오.

if) 구간의 길이가 5 일 때, 구간의 최대합은?

길이 6을 가지는 시작 지점(start) ~ 끝 지점(end)까지 합을 매번 더해서 구할 수 있습니다. 

(Sliding Window 혹은 Inchworm Algorithm)

직관적이지만 시간복잡도가 좋다고 할 수는 없습니다.

 

[O(N3) 코드]

int ans = 0;
int N, A[LM];
void findPartialSum(){
    int start, end, i;
    for(start = 1; start <= N; start++){
        for(end = start; end <= N; end++){
            int sum = 0;
            for(i = start; i<=end; i++){
                sum += A[i];
            }
            ans = ans < sum ? sum : ans;
        }
    }
}

 

합을 구하는 과정에서 조금 변형하여 O(N2)으로 구현도 가능

int ans = 0;
int N, A[LM];
void findPartialSum(){
    int start, end;
    for(start = 1; start <= N; start++){
        int sum =0;
        for(end = start; end <=N; end++){
            sum += A[end];
            if(ans < sum) ans = sum;
        }
    }
}

 

전체 코드

#include <iostream>
using namespace std;
const int N = 4;

void findPartialSum(int *arr) {
    int i, j, sum;
    for (i = 0; i < N; ++i){
        sum = 0;
        for (j = i; j < N; ++j){
            sum += arr[j];
            printf("[%d, %d]: %d\n", i, j, sum);
        }
    }
}

int main() {
    int arr[] = {2, 4, 6, 8};
    printf("[ ");
    for(int i=0; i<N; ++i){
        printf("%d ", arr[i]);
    }
    printf("]\n");
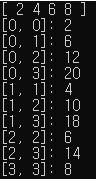
    findPartialSum(arr);
}

 

Reference

- 연속된 부분 합(연속합) - 1 (완전 탐색) 

- 연속된 부분 합(연속합) - 2 (Prefix Sum)

- 연속된 부분 합(연속합) - 3 (DP)  

- [구간합] Sum of sub-matrix (2D Array) 

 

관련 문제

- [BOJ] 2531 회전초밥