Sum of sub-matrix 란?
N × N와 같은 2차원 배열상에서 특정 영역의 합을 의미한다.

위에서 표시한 4 × 2 크기의 사각형이 가지고 있는 영역의 합은 어떻게 구할까?
Brute Force 방식으로 구한다면 아래와 같이 구할 수 있다.
#include <stdio.h>
const int N = 7;
int main()
{
int map[N][N] = {
{0, 0, 0, 0, 0, 0, 0},
{0, 1, 2, 3, 4, 5, 6},
{0, 2, 2, 2, 2, 2, 2},
{0, 3, 3, 3, 3, 3, 3},
{0, 4, 4, 4, 4, 4, 4},
{0, 5, 5, 5, 5 ,5 ,5},
{0, 6, 6, 6, 6, 6, 6},
};
int sx, sy, ex, ey;
sx = 2, sy = 4;
ex = 5, ey = 5;
for (int i = sx; i <= ex; ++i)
{
for (int j = sy; j <= ey; ++j)
{
printf("%2d ", map[i][j]);
}
puts("");
}
puts("");
}
주어진 사각형 범위를 아래 방식으로 표현 가능하다.

좌측 상단을 기준으로 height와 width를 이용하거나
(sx, sy) ~ (ex, ey)로 표현할 수 있다.
문제 상황
위와 같이 for문으로 해당 영역을 탐색한다면
height width가 크거나 해당 동작을 여러번 하는 경우에는 성능이 떨어질 수 밖에 없다.
ex) 2000 × 2000 크기에서 500 × 500 크기 영역을 여러번 탐색한다고 생각해보자.
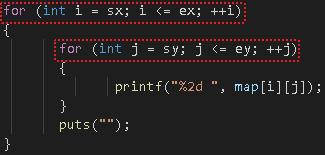
해당 영역의 상태를 출력해야 한다면 어쩔 수 없지만
해당 영역의 합을 구하는 것은 효율적인 방법이 존재한다. ▶ Sum of sub-matrix
Sum of sub-matrix 구현
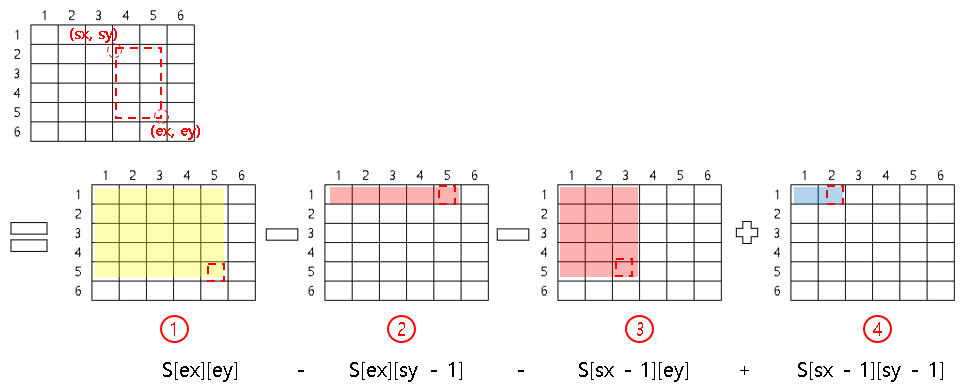
(1, 1) ~ (ex, ey)까지 부분합(①)에서 찾고자하는 영역이 아닌 곳을 제외한다.
→ 파랑색(④)은 빨강 (②와 ③)에서 중복적으로 제외된 부분을 한번 더해주는 것이다.
→ ① - ② - ③ + ④
→ (sx, sy) ~ (ex, ey) = S[ex][ey] - S[ex][sy - 1] - S[sx - 1][ey] + S[sx - 1][sy - 1]
Q) 그렇다면 (1, 1) ~ (x, y) 까지의 합은 어떻게 구하면 될까?
S[x][y] = S[x - 1][y] + S[x][y - 1] - S[x - 1][y - 1] + map[x][y]
#include <stdio.h>
const int MAX_N = 7;
int N = 6;
int S[MAX_N][MAX_N];
void printState(int arr[MAX_N][MAX_N], int size_t)
{
for (int i = 1; i <= size_t; ++i)
{
for (int j = 1; j <= size_t; ++j)
{
printf("%2d ", arr[i][j]);
}
puts("");
}
puts("");
}
int main()
{
int map[MAX_N][MAX_N] = {
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
};
for (int y = 1; y <= MAX_N; ++y)
{
for (int x = 1; x <= MAX_N; ++x)
{
S[x][y] = S[x - 1][y] + S[x][y - 1] - S[x - 1][y - 1] + map[x][y];
}
}
printState(S, N);
}
- 부분합 결과를 쉽게 확인하기 위해 map[][]을 "0"과 "1" 로 구성
- S[][]를 구할 때, for문 방향 유의
※ 0 행과 0 열은 값이 "0"이므로 인덱스 접근과 계산에 영향을 미치지 않는다
S[][] 이용해서 Sum of sub-matrix 구하기
S[][]를 구했다면, map[][]에서 크기와 횟수 제한에 자유로워진다.
아래와 같이 표시된 영역 (2, 2) ~ (5, 3)의 합을 구해보자.
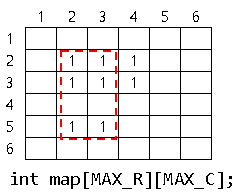
"0" 혹은 "1" 로 구성되었기 때문에 쉽게 1 + 1 + 1+ 1 + 1 + 1 = 「 6 」을 알 수 있다.
이는 아래와 같이 표현할 수 있다.
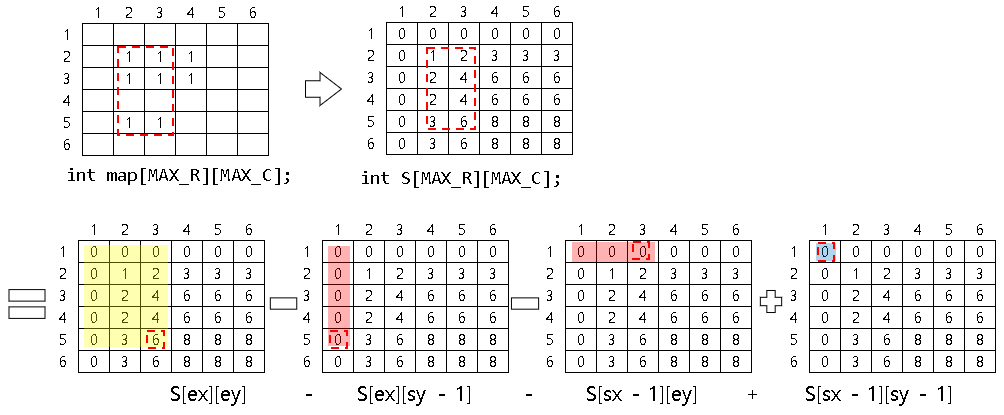
▶ (sx, sy) ~ (ex, ey) = S[ex][ey] - S[ex][sy - 1] - S[sx - 1][ey] + S[sx - 1][sy - 1]
(2, 2) ~ (5, 3) = S[5][3] - S[5][1] - S[1][3] + S[1][1] = 6 - 0 - 0 + 0 = 6
#include <stdio.h>
const int MAX_N = 7;
int N = 6;
int S[MAX_N][MAX_N];
void printState(int arr[MAX_N][MAX_N], int size_t)
{
for (int i = 1; i <= size_t; ++i)
{
for (int j = 1; j <= size_t; ++j)
{
printf("%2d ", arr[i][j]);
}
puts("");
}
puts("");
}
int main()
{
int map[MAX_N][MAX_N] = {
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
};
for (int y = 1; y <= MAX_N; ++y)
{
for (int x = 1; x <= MAX_N; ++x)
{
S[x][y] = S[x - 1][y] + S[x][y - 1] - S[x - 1][y - 1] + map[x][y];
}
}
printState(S, N);
}
활용
아래와 같이 ①, ② 자리에 새로운 사각형을 놓고자 한다.
이때, 기존 map[][]을 덮어씌우지 않고 "0"곳만 가능하다고 했을 때,
→ 해당 영역을 for문으로 탐색해서 알아본다면 성능이 좋지 못하다.
→ 각각의 Sum of sub-matrix 값이 어떻게 되는지 살펴보자.
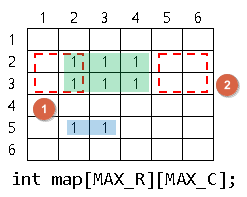
① (sx, sy) ~ (ex, ey) = S[ex][ey] - S[ex][sy - 1] - S[sx - 1][ey] + S[sx - 1][sy - 1]
(2, 1) ~ (3, 2) = S[3][2] - S[3][0] - S[1][2] + S[1][0]
= 2 - 0 - 0 + 0 = 2 → "불가능"

② (sx, sy) ~ (ex, ey) = S[ex][ey] - S[ex][sy - 1] - S[sx - 1][ey] + S[sx - 1][sy - 1]
(2, 5) ~ (3, 6) = S[3][6] - S[3][4] - S[1][6] + S[1][4]
= 6 - 6 - 0 + 0 = 0 → "가능"

▶ 결과가 "0" 인지로 판단할 수 있다
▶ 부분합은 Problem Solving(PS)에서 가끔 활용할 수 있는 기법이다.
#include <stdio.h>
const int MAX_N = 7;
int N = 6;
int S[MAX_N][MAX_N];
struct Node {
int x, y;
void alloc(int x, int y)
{
this->x = x; this->y = y;
}
}s, e;
void printState(int arr[MAX_N][MAX_N], int size_t)
{
for (int i = 1; i <= size_t; ++i)
{
for (int j = 1; j <= size_t; ++j)
{
printf("%2d ", arr[i][j]);
}
puts("");
}
puts("");
}
int sumOfSubMatrix()
{
#if 0
printf("%d - %d - %d + %d\n", S[e.x][e.y], S[e.x][s.y - 1],
S[s.x - 1][e.y], S[s.x - 1][s.y - 1]);
#endif
return S[e.x][e.y] - S[e.x][s.y - 1] - S[s.x - 1][e.y] + S[s.x - 1][s.y - 1];
}
int main()
{
int map[MAX_N][MAX_N] = {
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0},
};
for (int y = 1; y <= MAX_N; ++y)
{
for (int x = 1; x <= MAX_N; ++x)
{
S[x][y] = S[x - 1][y] + S[x][y - 1] - S[x - 1][y - 1] + map[x][y];
}
}
printState(S, N);
s.alloc(2, 2); e.alloc(5, 3);
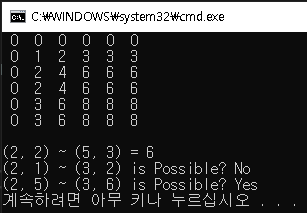
printf("(%d, %d) ~ (%d, %d) = %d\n", s.x, s.y, e.x, e.y, sumOfSubMatrix());
s.alloc(2, 1); e.alloc(3, 2);
printf("(%d, %d) ~ (%d, %d) is Possible? %s\n", s.x, s.y, e.x, e.y, sumOfSubMatrix() == 0 ? "Yes" : "No");
s.alloc(2, 5); e.alloc(3, 6);
printf("(%d, %d) ~ (%d, %d) is Possible? %s\n", s.x, s.y, e.x, e.y, sumOfSubMatrix() == 0 ? "Yes" : "No");
}
Reference
- 연속된 부분 합(연속합) - 2 (Prefix Sum)

'알고리즘' 카테고리의 다른 글
| [알고리즘] 시간 성능 향상을 위한 코드 최적화 (C/C++) (0) | 2021.05.05 |
|---|---|
| [알고리즘] 코딩 테스트 문제 풀 때, 시간 복잡도 계산해보기 (2) | 2021.05.05 |
| 힙 정렬 (Heap Sort) (0) | 2021.03.06 |
| Binary Search (이분 탐색) (0) | 2021.03.06 |
| 계수 정렬(Counting Sort) (0) | 2021.03.06 |





댓글