Binary Search (이분 탐색)
정렬된 자료에서 목표값을 찾고자 할 때, 사용되는 탐색기법 O(logN)
리스트 중간의 값(mid)을 선택하여 찾고자 하는 값과 비교하는 방식
분할 정복 알고리즘(Divide and Conquer Algorithm)
주어진 문제의 크기가 감당하기 어려운 경우 보다 작은 문제로 나누어 해결하는 방법(알고리즘)
이진검색, 퀵정렬, 합병정렬 등이 대표적인 예이다.
ex) 원소 『41』 을 찾아가는 과정

이진 검색 과정
정렬된 데이터 배열 A[ ]가 주어지고 목표값(target)을 찾는다고 가정해보자.
이때, 첫 번째 원소의 인덱스는 low이고, 마지막 원소의 인덱스는 high 라고 하자.
① 현재 탐색 구간의 가운데 배열 번호(인덱스) mid 구한다.
mid = (low + high) / 2;
② A[mid] 값과 target 비교
→ A[mid] == target 이라면 목표 값 또는 목표 값이 있는 위치를 찾은 것
→ A[mid] < target 이라면 low = mid + 1로 하여 검색 범위 조정
검색 범위가 절반 이하로 줄어들었다.
→ 만약 A[mid] > target 이라면 high = mid -1로 하여 검색 범위 조정
마찬가지로 검색 범위가 절반 이하로 줄어들었다.
③ 탐색 구간이 남아있고 목표값을 찾지 못한 동안 프로세스 반복
만약 low > high 라면 (탐색 구간이 남지 않은 경우) 목표 값이 배열에 없는 경우
Loop-version
int binarySearch(int *arr, int low, int high, int target) {
while (low <= high) {
int mid = (low + high) / 2;
if (arr[mid] == target)
return mid;
if (arr[mid] < target)
low = mid + 1;
else
high = mid - 1;
}
// 찾지 못한 경우
return -1;
}
recursive-version
int binarySearch(int *arr, int low, int high, int target) {
// 찾지 못한 경우
if (low > high) return -1;
int mid = (low + high) / 2;
// 목표값을 찾은 경우
if (arr[mid] == target) return mid;
// 목표 값이 중간위치보다 큰 쪽에 있을 것으로 예상
if (arr[mid] < target) {
return binarySearch(arr, mid + 1, high, target);
}
// 목표 값이 중간위치보다 작은 쪽에 있을 것으로 예상
return binarySearch(arr, low, mid - 1, target);
}
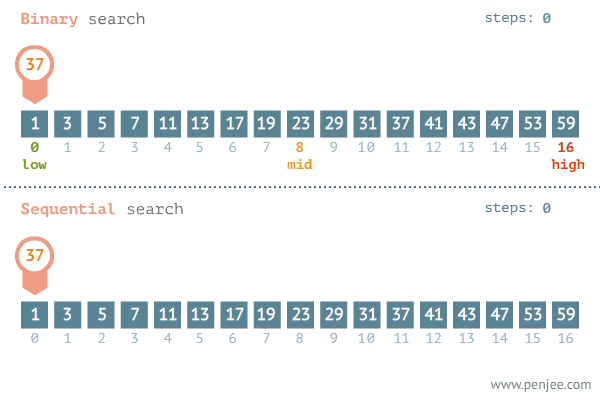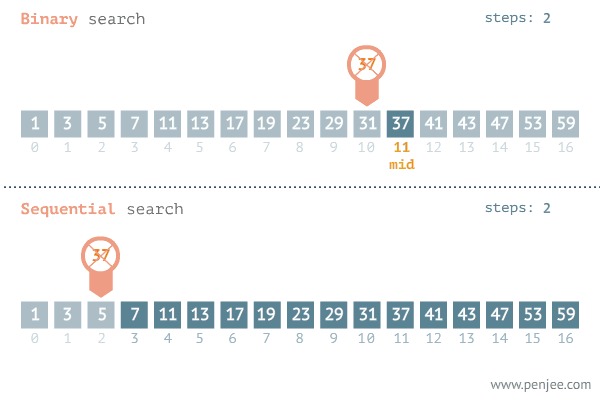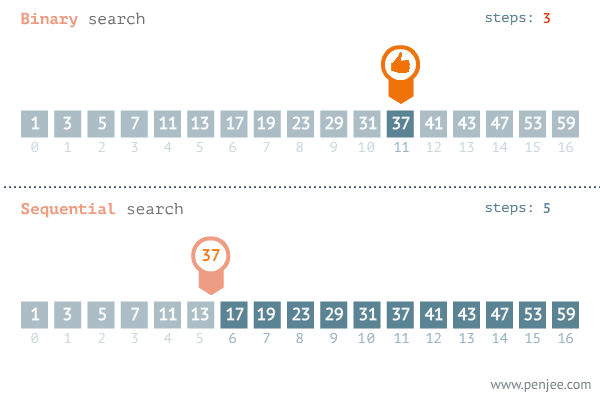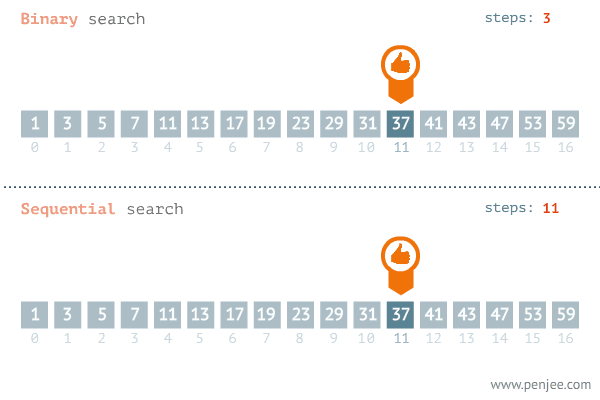
이분탐색과 선형탐색 비교
이진 검색을 PS에 적용하는 경우
- 최적화 문제를 결정 문제로 바꿔서 생각하는 경우가 많음
- 결정 문제의 참/거짓의 결과 이용
- 이분검색으로 가장 최적의 해 검색
Reference
- [Jungol] 3517 Tutorial : 이진탐색(Binary Search-이진검색)
- [Jungol] 2543 타일 채우기 ( + 분할정복)
- [SWEA] 9236 곰돌이 (BFS + 이분탐색, Upper Bound)

'알고리즘' 카테고리의 다른 글
| [구간합] Sum of sub-matrix가 무엇이고, 어떻게 하는 것일까? (0) | 2021.05.03 |
|---|---|
| 힙 정렬 (Heap Sort) (0) | 2021.03.06 |
| 계수 정렬(Counting Sort) (0) | 2021.03.06 |
| LCP (Longest Common Prefix) (0) | 2021.03.06 |
| [탐색] Parametric Search (0) | 2021.03.04 |





댓글