힙 정렬 (Heap Sort)
- O(N logN)
▶ [그래프] 힙(Heap) 구조를 이용해서 정렬합니다.
힙(Heap) 자료구조란?
Heap - 최대값 또는 최소값을 빠르게 구하기 위한 자료구조 - 완전 이진 트리를 기본으로 한 자료구조 - 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다. - 트리가 한쪽으로 기울어진
zoosso.tistory.com
▶ 더 많은 예제: 힙 정렬
[예제] 힙 정렬 구현
Heap Sort ▶ Heap 구조가 궁금한 경우 [그래프] 힙(Heap) 힙(Heap) 자료구조란? Heap - 최대값 또는 최소값을 빠르게 구하기 위한 자료구조 - 완전 이진 트리를 기본으로 한 자료구조 - 마지막 레벨을
zoosso.tistory.com
구현
① 주어진 원소를 Heap 구조로 만듭니다.
배열의 인덱스를 이용해 원소의 순서 변경만으로 Heap 구조를 만들 수 있습니다.
Heap 구조를 만드는 과정을 『Heapify』 라고 합니다.

위의 주어진 원소를 아래 Max Heap 구조로 변경
- (Max Heap) 최상위 노드인 루트 노드는 전체 원소 중에서 항상 최대값을 가집니다.
- 부모 노드 ≥ 자식 노드

② Heap에서 Root Node와 마지막 노드의 위치를 바꿔줍니다.
③ 배열(Heap)의 크기를 줄여가며 변경된 Root Node에 대해서 Heap을 재구성합니다.
재구성된 Heap에서는 마찬가지로 원소들의 최대값이 위치합니다.
②, ③을 Heap의 크기가 1보다 크면 반복

위치를 swap()하여 Root Node = 2 / 마지막 원소에 15로 위치 변경

마지막 원소에 위치한 15를 제외하고 Heap을 재구성 합니다.
부모노드 2 < 자식노드 14, 13 이므로 자식노드 중 더 큰 값 14와 자리 변경

부모노드 2 < 자식노드 12, 7 이므로 자식노드 중 더 큰 값 12와 자리 변경
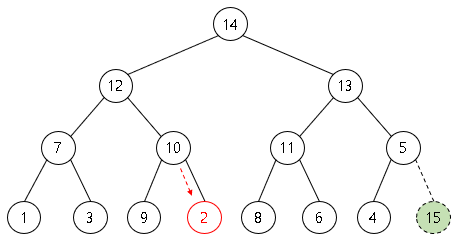
부모노드 2 < 자식노드 10, 9 이므로 자식노드 중 더 큰 값 10과 자리 변경

위치를 swap()하여 Root Node = 4 / 현재 Heap상에 마지막 위치에 14로 변경
새로운 Root Node = 4에 대해서 Heap 재구성 (내려가는 과정을 Down Heap 이라고 합니다.)

위와 같이 초기 크기 N번만큼 반복하면 진행과정에서 Heap 마지막 위치에
내림차순으로 노드들이 쌓이게 됩니다.

힙 정렬은 Heap에서 원소들을 꺼낼 때 항상 최대값 or 최소값을 반환하는 특성을 이용합니다.
이때 Heap에서 원소를 하나 꺼내면 Heap을 담은 배열의 맨 뒤쪽에 한 칸이 비게 되므로
최대 원소를 여기에 옮겨주기에 추가 메모리를 사용하지 않고 정렬을 구현할 수 있습니다.
Code
#include <stdio.h>
int swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
void heapify(int array[], int n, int i) {
int parentNode = i;
int leftChildNode = i * 2 + 1;
int rightChildNode = i * 2 + 2;
// 왼쪽 자식 노드가 존재하면서 부모노드와 값 비교.
if (leftChildNode < n && array[parentNode] < array[leftChildNode]) {
parentNode = leftChildNode;
}
// 오른쪽 자식 노드가 존재하면서 부모노드와 값 비교.
if (rightChildNode < n && array[parentNode] < array[rightChildNode]) {
parentNode = rightChildNode;
}
// 왼쪽 or 오른쪽 자식 노드 중 부모 노드보다 큰 값이 존재한 경우
if (i != parentNode) {
swap(&array[parentNode], &array[i]);
// 초기 부모노드가 제자지를 찾을 때까지 내려갑니다.
heapify(array, n, parentNode);
}
}
void heapSort(int array[], int n) {
// 최대 힙(Max Heap) 구성
for (int i = (n / 2) - 1; i >= 0; i--) {
heapify(array, n, i);
}
// Root에 위치한 최대값을 마지막 노드와 바꿔가며 Heap 재구성
// Heap의 크기를 줄여가며 값이 큰 원소를 차례로 가져옵니다.
for (int i = n - 1; i > 0; i--) {
swap(&array[0], &array[i]);
heapify(array, i, 0);
}
}
void main(void) {
int n = 9;
int array[9] = { 7, 6, 5, 8, 3, 5, 9, 1, 6 };
heapSort(array, n);
// 오름차순 출력
for (int i = 0; i < n; i++) {
printf("%d ", array[i]);
}
}
'알고리즘' 카테고리의 다른 글
| [알고리즘] 코딩 테스트 문제 풀 때, 시간 복잡도 계산해보기 (2) | 2021.05.05 |
|---|---|
| [구간합] Sum of sub-matrix가 무엇이고, 어떻게 하는 것일까? (0) | 2021.05.03 |
| Binary Search (이분 탐색) (0) | 2021.03.06 |
| 계수 정렬(Counting Sort) (0) | 2021.03.06 |
| LCP (Longest Common Prefix) (0) | 2021.03.06 |





댓글