반응형
★ 에라토스테네스의 체의 핵심은 소수의 배수를 제외 시키는 것이다.
출처: WIKI
▶ 다음과 같이 2~50까지의 숫자가 존재한다.
(1은 소수가 아니므로 제외)

▶ 먼저, 『2』의 소수 여부를 판단한다.
소수라면 『2』의 배수를 모두 제외시킨다.
(『2』로 나누어지는 합성수들이기 때문.)

▶ 마찬가지로 『3』에 대해서도 동일하게 처리하면 다음과 같다.

▶ 『4』는 앞서 『2』의 배수에서 처리되었으므로 넘어간다.
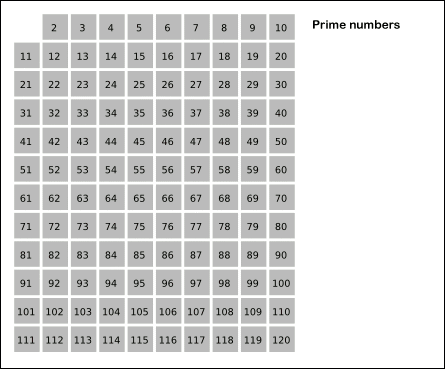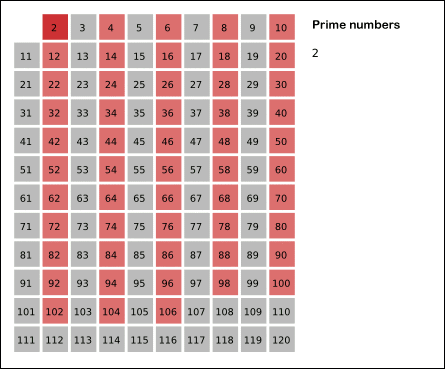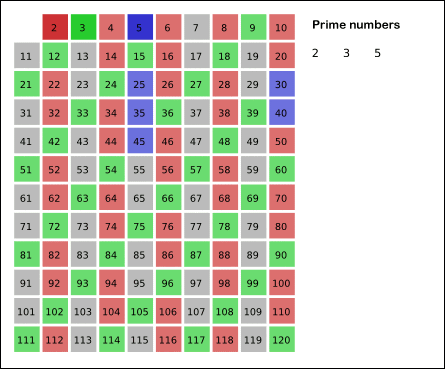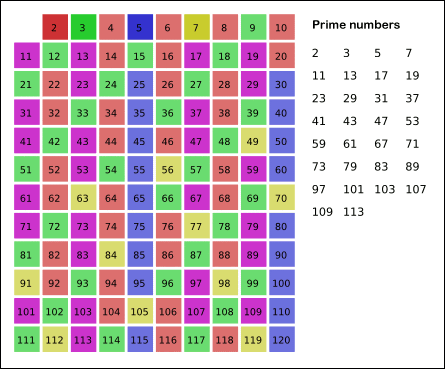
▶ 이러한 방법으로 소수의 배수를 제외 시키면 소수 여부를
판단하는 대상이 좁혀지기 때문에 효율적이다.
결과적으로 아래 숫자에 대해서만 소수 검증이 이루어진다.

[Java]
public class Main {
public static void main(String[] args) {
long startTime = System.currentTimeMillis();
int N = 100000000;
int arr[] = new int[N + 1];
arr[1] = 1; // 1은 소수가 아니다.
for(int i=2; i*i<=N; i++){
// 에라토스테넷스의 체
if(arr[i] == 0){
// 배수들을 제외 처리.
for(int j=2; i*j<=N; j++){
arr[i*j] = 1;
}
}
}
int cnt = 0;
for(int i=2; i<=N; i++){
if(arr[i] == 0){
cnt++;
}
}
long endTime = System.currentTimeMillis();
System.out.println("2 ~ N 까지 소수 개수: " + cnt);
System.out.println( "경과시간: " + (endTime - startTime));
}
}[2~100000까지 소수 개수 및 경과시간 확인]

아래 3가지 방식을 수행 시간으로 비교하면
① 2 ~ N-1 까지 나누어지는지 확인
② 2 ~ √N 까지 나누어지는지 확인
③ 에라토스테네스의 체
▶ { ③ 2 } > { ② 12 } > { ① 1390 } 수치를 확인할 수 있다.
* 연산 범위 및 디버깅 환경에 따라 다를 수 있다.
[관련 문제]
- [BOJ] 1929 소수 구하기 (Java)
- [BOJ] 2960 에라토스테네스의 체 (C / C++)

반응형
'알고리즘' 카테고리의 다른 글
| [문자열] KMP 알고리즘 (0) | 2021.02.22 |
|---|---|
| LCS(Longest Common Subsequence) 알고리즘 (0) | 2021.02.21 |
| 소수 (Prime Number) 찾기 - 2 (0) | 2021.02.21 |
| 소수(Prime Number) 찾기 - 1 (0) | 2021.02.20 |
| 연속된 부분 합(연속합) - 1 (완전 탐색) (0) | 2021.02.20 |





댓글