LCS(Longest Common Subsequence) 알고리즘

LCS(Longest Common Subsequence) '최장 공통 부분 수열'로

연속된 부분 문자열 Substring과는 다른 개념이다.

   ▶ [BOJ] 5582 공통 부분 문자열

가령, 아래 두 문자열이 주어졌을 때,

- A    B    C    D    H    E    F           

- B    C    D    E    F

→ 최장 공통 Substring 'BCD'

→ 최장 공통 Subsequence는 'BCDEF'

 

LCS를 DP를 통해 해결할 수 있다.

 

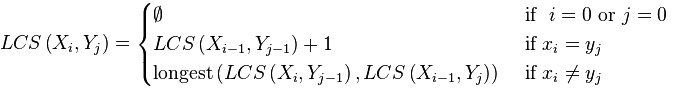
도표를 통해 해석해보겠다.

ACAYKP

CAPCAK

A[i] == B[j] 인 경우, LCS[i][j] = LCS[i][j] + 1;

A[i] != B[j] 인 경우, Math.max(LCS[i-1][j], LCS[i][j-1])

 

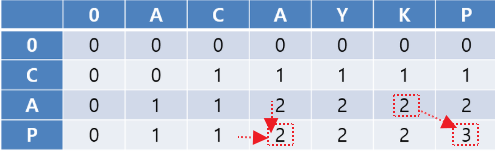
LCS의 길이는 마지막 값을 출력하면 된다.

LCS의 길이(크기) 출력하는 문제는 아래 참고

- [BOJ] 9251 LCS

- [BOJ] 1958 LCS 3

 

그렇다면 실제 LCS의 문자열을 어떻게 찾을 수 있을까?

완성된 도표를 이용하면 쉽게 찾을 수 있다.

① 마지막 지점 (x, y)에서 부터 출발한다. 

② A[x] == B[y] 이면, 대각선 방향으로 좌측상단 이동한다.

③ A[x] != B[y] 이면, 현재 LCS[x-1][y], LCS[x][y-1] 중에서 같은 값이 있는 방향으로 이동

④ x == 0 || y ==0 일 때까지 과정 ①~③을 반복. (LCS[x][y] == 0 인 지점)

⑤ 일치했던 문자를 역순으로 출력한다.

 

LCS의 길이와 함께 실제 공통 문자열을 출력하는 문제

- [BOJ] 9252 LCS 2