문자열 Hash 고찰
문자열 Hash (djb2)에서 문자열 → 정수로 변환해서
Hash 구현이 가능해진 것을 확인할 수 있었다.
unsigned long djb2(const char* str)
{
unsigned long hash = 5381;
int c;
while (c = *str++)
{
hash = (((hash << 5) + hash) + c) % TABLE_SIZE;
}
return hash % TABLE_SIZE;
}Q) djb2 함수는 Hash 충돌이 얼마나 발생할까?
→ djb2 함수는 key 효과적으로 분산시킬 수 있다고 한다.
→ 하지만 Hash Key 충돌 발생하지 않는 것을 보장할 수 없기에
Hash 충돌 처리를 해야 한다. → <Chaining> or <Open Address 기법>
[해시] Hash Open Address 기법 구현
[해시] Hash란?에 작성한 Hash를 구현하는 방식 중 하나인 체이닝(Chaining) 기법을 구현하였습니다. Hash 개념이 필요하신 분은 먼저 [해시] Hash란?을 참고해주세요 Open Address 기법 Hash Function이나 주어.
zoosso.tistory.com
[해시] Hash Chaining 기법 구현
[해시] Hash란?에 작성한 Hash를 구현하는 방식 중 하나인 체이닝(Chaining) 기법을 구현하였습니다. Hash 개념이 필요하신 분은 먼저 [해시] Hash란?을 참고해주세요 Chaining 기법 Hash Function이나 주어지
zoosso.tistory.com
Q) djb2 함수에서 "5381" 숫자가 어떤 의미일까?
Q) djb2 함수에서 "5381" 숫자가 어떤 의미일까?
→ djb2 함수에서 5381은 일종의 "Magic Number" 라고 한다.
→ 평균적으로 문자열들을 잘 분산시킬 수 있는 수치라고 한다.
물론, 문제 상황에 따라 더 적합한 수치가 있겠지만
5381은 수치적으로 시뮬레이션 해서 얻은 수치이다.
→ 일반적으로 소수가 좋다. ("5381"도 709th Prime Number 이다.)
→ 5381을 2진법으로 표현하면 "0101 0011 1000 0001" 이다.
→ 홀수 (Odd Number)
→ 부족 수 (Deficient Number)
Q) Hash 문제 풀이 시, 어떻게 접근하면 좋을까?
→ STL 사용하지 못하면서 문자열 Hash를 구현하는 상황에서 적용할 수 있다.
문제 조건에 따라서는 알파벳을 직접적으로 Decoding 해서 key를 구할 수도 있다.
※ 계속 되는 내용에서 아스키 코드를 이용한 Decoding 방식과 djb2 함수를 활용한 방식 참고
문제 상황
- 소문자(a-z)로 이루어진 Uniqu한 문자열 이름(name)
- 문자열의 길이는 1 ~ 3 글자
▶ "a" ~ "zzz"
ex) "har", "cow", "pig"
문자열 Data 생성
소문자로 구성된 길이가 최소 1에서 최대 3 이므로
"a" ~ "zzz" 까지 구성되는데, 아스키 코드 + 중복을 허용하는 순열로 구할 수 있다.
▶ N과 M (3)
▶ 순열과 조합
#include <stdio.h>
const int MAX_N = 8 + 2;
int N, len, ans[MAX_N], cnt;
void DFS(int depth) {
if (depth == len) {
printf("[%d] ", ++cnt);
for (int i = 0; i < len; ++i) {
printf("%c ", ans[i] + 96);
}
printf("\n");
return;
}
for (int i = 1; i <= N; ++i) {
ans[depth] = i;
DFS(depth + 1);
ans[depth] = 0;
}
}
int main() {
N = 26;
for (int l = 1; l <= 3; l++)
{
// 26개의 알파벳 중 l 개 선택
len = l;
DFS(0);
}
}
- 1글자: 26
- 2글자: 26 × 26 = 676
- 3글자: 26 × 26 × 26 = 17,576
▶ 26 + 676 + 17,575 = 18,278
Decode
소문자 알파벳은 a ~ z 까지 26 글자로 이루어져 있다.
최소 1 글자에서 최대 3 글자 이므로 나올 수 있는 경우의 수는 18,278개
Q) 아스키코드를 토대로 "cow" 어떻게 전환시킬 수 있을까?
"cow" → c = 3번째, o = 15번째, w = 23번째 알파벳인데
c = 3 × 262 = 2,028
o = 15 × 261 = 390
w = 23 × 260 = 23
▶ 2028 +
390+ 23 = 2,441
몇 개 더 살펴보면 아래와 같다.
"ba" → (2 × 26) + (1) = 53
"zzz" → (26 × 262) + (26 × 26) + (26) = 18,278
- a ~ zzz 까지의 Input Data를 decode() 함수로 Hash Key 값을 구한다.
- tbl[key]에서 이미 값이 존재한다면 충돌 → crushCnt++;
#include <stdio.h>
const int TABLE_SIZE = 18278 + 1;
const int MAX_N = 8 + 2;
int N, len, ans[MAX_N], cnt, crushCnt;
char str[MAX_N];
int tbl[TABLE_SIZE];
unsigned long decode(const char* str)
{
unsigned long hash = 0;
int c = 1;
// 앞글자부터 Decoding
for (int i = len - 1; i >= 0; i--)
{
hash += (str[i] - 96) * c;
c *= N;
}
return hash % TABLE_SIZE;
}
void DFS(int depth) {
if (depth == len) {
++cnt;
// 아스키 코드를 토대로 문자열 구성
for (int i = 0; i < len; ++i) {
str[i] = ans[i] + 96;
}
// Hash Function으로 key 값 반환
int key = decode(str);
// 충돌 여부 확인
if (tbl[key] >= 1)
{
crushCnt++;
return;
}
tbl[key] = 1;
return;
}
for (int i = 1; i <= N; ++i) {
ans[depth] = i;
DFS(depth + 1);
ans[depth] = 0;
}
}
int main() {
N = 26;
for (int l = 1; l <= 3; l++)
{
// 26개의 알파벳 중 l 개 선택
len = l;
DFS(0);
}
if (crushCnt > 0)
printf("%d개 충돌 발생!!\n", crushCnt);
else
printf("충돌 X\n");
}
- Input Data 개수와 충돌이 나지 않게 Decoding 할 수 있기에
Hash Table의 크기를 계산할 수 있었다. → tbl[18278 + 1]
- Key 충돌 발생하지 않는 것이 보장되기에 Chaining이나 Open Addressing 처리하지 않아도 된다.
이는 반대로 정확하게 계산해서 Hash Table 크기를 정할 필요가 있다.
djb2 함수
- Hash Function에 해당하는 함수 변경
decode() → djb2()
#include <stdio.h>
const int TABLE_SIZE = 18278 + 1;
const int MAX_N = 8 + 2;
int N, len, ans[MAX_N], cnt, crushCnt;
char str[MAX_N];
int tbl[TABLE_SIZE];
unsigned long djb2(const char* str)
{
unsigned long hash = 5381;
int c;
while (c = *str++)
{
hash = (((hash << 5) + hash) + c) % TABLE_SIZE;
}
return hash % TABLE_SIZE;
}
void DFS(int depth) {
if (depth == len) {
++cnt;
// 아스키 코드를 토대로 문자열 구성
for (int i = 0; i < len; ++i) {
str[i] = ans[i] + 96;
}
// Hash Function으로 key 값 반환
int key = djb2(str);
// 충돌 여부 확인
if (tbl[key] >= 1)
{
crushCnt++;
return;
}
tbl[key] = 1;
return;
}
for (int i = 1; i <= N; ++i) {
ans[depth] = i;
DFS(depth + 1);
ans[depth] = 0;
}
}
int main() {
N = 26;
for (int l = 1; l <= 3; l++)
{
// 26개의 알파벳 중 l 개 선택
len = l;
DFS(0);
}
if (crushCnt > 0)
printf("%d개 충돌 발생!!\n", crushCnt);
else
printf("충돌 X\n");
}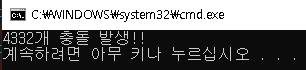
Hash Function만 변경했는데, Key 충돌 되는 것을 확인할 수 있다.
djb2 함수는 TABLE_SIZE 크기에 따라 충돌횟수를 조절할 수 있다.
<TABLE_SIZE의 값에 따른 충돌 개수>
const int TABLE_SIZE = 1 << 16; ▶380번 충돌
const int TABLE_SIZE = 1 << 17; ▶19번 충돌
const int TABLE_SIZE = 1 << 18; ▶충돌 X
결론
코딩 테스트에서 문자열 Hash를 직접 구현할 때,
문제 조건을 분석해서 Key 충돌이 발생하지 않도록 Decoding 한다면
Hash 성능을 최적화할 수 있다.
하지만 제한된 시간에서 계산하는 것을 확신할 수 없다면
djb2 함수로 Hash Function을 처리하고, key 충돌 처리 Code를 구현하는 것이 안정적일 것 같다.
Reference
- 순열과 조합
- [해시] Hash Open Address 기법 구현
- Hash 구현 (양방향, 더미노드 0개, *head)
- Hash (양방향, 더미노드 2개, *head, *tail)
- Hash (양방향, 더미노드 2개, head, tail)

'알고리즘' 카테고리의 다른 글
| 재귀(Recusion) 함수? 재귀 호출(Recusive Call)? (0) | 2021.07.24 |
|---|---|
| 완전탐색 기법이란? (0) | 2021.07.24 |
| 문자열 Hash (djb2) (0) | 2021.06.12 |
| [예제] 힙 정렬 구현 (0) | 2021.06.04 |
| [예제] 퀵 정렬 구현 (0) | 2021.06.04 |





댓글