[해시] Hash란?에 작성한 Hash를 구현하는 방식 중 하나인
체이닝(Chaining) 기법을 구현하였습니다.
Hash 개념이 필요하신 분은 먼저 [해시] Hash란?을 참고해주세요
Open Address 기법
Hash Function이나 주어지는 Input Data에 따라 key간 Hash Index 충돌이 일어날 수 있다.
아래 그림과 같이 ▶ Hash Function = key mod 11 일 때,
data = {8, 19, 30}은 동일한 Hash Index = "8" 을 가진다.

- 동일한 Hash Index를 가질 때, Hash Table의 비어있는 곳을 찾아서 해결할 수 있다.
- Chaining 기법과 달리 추가 메모리 할당이 없다.
(Input Data 개수는 초기 Hash Table 크기에 의존적이다.)
- Key의 정확한 Hash Index 값을 예측할 수 없다.
- 주소 개방 기법에는 선형 조사 / 이차원 조사 / 이중 해싱 등이 존재
구현 함수 설명
Init
void Init(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
hTbl[i].value = EMPTY;
}
}- 구조체 배열로 만들어진 Hash Table 값을 비어있는(Empty) 표시 처리
PrintHash
void PrintHash(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
printf("[%2d]: ", i);
if (hTbl[i].value != EMPTY)
{
printf("%d", hTbl[i].value);
}
puts("");
}
puts("");
}- 원래 비어있거나 삭제되어서 비어진 곳이 아닌 경우 값을 출력
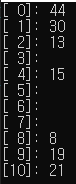
Insert
int Insert(Node* data)
{
int pos, key;
pos = key = GetKey(data->value);
for (;;)
{
if (hTbl[pos].value == EMPTY)
{
hTbl[pos] = *data;
return pos;
}
pos += STEP;
if (pos == key) // One Cycle을 돌아서 출발위치 다시 도달한 경우
return FAIL; // Hash Table이 가득찬 상태 (FULL)
if (pos >= HASH_SIZE) // 시작위치를 첫번째 인덱스로 설정
pos = 0;
}
}- 처음 key 맞는 Hash Index에 접근했을 때, 충돌이 발생한 경우
비어있는 곳을 찾아야 한다.
- 이때, Hash Size를 순환할 수 있도록 탐색 Index 유의해야 한다.
- 탐색 범위는 처음 출발한 Hash Index부터해서 한 바퀴를 돌아 출발점으로 돌아오는 경우이다.

위와 같이 중간에 비어있는 Hash Index가 확인되면 그곳에 안착하게 된다.
그렇기에 Open Address는 쌓여져 있는 Data에 따라 정확한 Hash Index를 예측하기 어렵다.
→ 적은 데이터가 여러번 접근될 때 적합한 기법이라고 볼 수 있다.
(※ 참조 지역성이란? Locality of reference, 하나의 자원에 여러번 접근하는 프로세스)
Search
Node* Search(int value)
{
int pos, key;
pos = key = GetKey(value);
for (;;)
{
if (hTbl[pos].value == value)
return &hTbl[pos];
if (hTbl[pos].value == EMPTY)
return (Node*)0; // 찾지 못한 경우
pos += STEP;
if (pos == key)
return (Node*)0;
if (pos >= HASH_SIZE)
pos = 0;
}
}Search()는 일치하는 값을 한 바퀴 돌면서 탐색하되
출발점으로부터 다시 출발점으로 돌아올 때까지 모두 탐색할 필요 없이
중간에 비어있는 곳이 발견된다면 더 이상의 탐색은 무의미하므로 종료한다. (분기한정)
Remove
int Remove(int id)
{
Node *p = Search(id);
if (p == (Node*)0)
return FAIL; // 원소를 찾지 못한 경우
p->value = EMPTY;
return SUCCESS;
}구현한 Search() 함수를 이용해서 대상을 찾은 경우에만 다시 비워준다.
전체 코드
- [해시] Hash Chaining 기법 구현의 main() 내용은 다르지 않고
Hash 구조 방식에 차이가 있다.
#include <stdio.h>
const int MAX_N = 7;
const int HASH_SIZE = 11;
const int STEP = 1;
const int EMPTY = -1;
const int SUCCESS = 1;
const int FAIL = -3;
struct Node
{
int value;
}hTbl[HASH_SIZE];
Node data[] = { {44}, {13}, {15}, {8}, {21}, {19}, {30} };
int GetKey(int id)
{
return id % HASH_SIZE;
}
void Init(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
hTbl[i].value = EMPTY;
}
}
void PrintHash(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
printf("[%2d]: ", i);
if (hTbl[i].value != EMPTY)
{
printf("%d", hTbl[i].value);
}
puts("");
}
puts("");
}
int Insert(Node* data)
{
int pos, key;
pos = key = GetKey(data->value);
for (;;)
{
if (hTbl[pos].value == EMPTY)
{
hTbl[pos] = *data;
return pos;
}
pos += STEP;
if (pos == key) // One Cycle을 돌아서 출발위치 다시 도달한 경우
return FAIL; // Hash Table이 가득찬 상태 (FULL)
if (pos >= HASH_SIZE) // 시작위치를 첫번째 인덱스로 설정
pos = 0;
}
}
Node* Search(int value)
{
int pos, key;
pos = key = GetKey(value);
for (;;)
{
if (hTbl[pos].value == value)
return &hTbl[pos];
if (hTbl[pos].value == EMPTY)
return (Node*)0; // 찾지 못한 경우
pos += STEP;
if (pos == key)
return (Node*)0;
if (pos >= HASH_SIZE)
pos = 0;
}
}
int Remove(int id)
{
Node *p = Search(id);
if (p == (Node*)0)
return FAIL; // 원소를 찾지 못한 경우
p->value = EMPTY;
return SUCCESS;
}
void main(void)
{
Init();
for (int i = 0; i < MAX_N; i++)
{
Insert(&data[i]);
}
PrintHash();
int target = 19;
if (Node* p = Search(target))
{
printf("탐색 결과 %d 는 존재.\n", p->value);
}
else
{
printf("탐색 결과 존재하지 않습니다.\n", target);
}
printf("\n=== 삭제 후 상태===\n");
if (Remove(19))
{
PrintHash();
}
if (Node* p = Search(target))
{
printf("탐색 결과 %d 는 존재.\n", p->value);
}
else
{
printf("%d를 탐색 결과 존재하지 않습니다.\n\n", target);
}
}
삭제 방식 변경에 따른 처리
이전까지 보여준 Code에서는 Hash Table의 Node를 삭제하면 "EMPTY(-1)" 상태로 만들었다.
비어있는 상태로 만든 것인데, 삭제 여부를 다른 값으로 덮어씌우는 것으로 처리할 수 있다.
ex) 삭제 표시를 DELETED(-2)로 표시
→ 삭제된 곳을 구분할 수 있다.
삭제하는 방식에 따라 다른 함수도 다시 고려해주어야 한다.
→ Insert()와 PrintHash() 내용 변경
#include <stdio.h>
const int MAX_N = 7;
const int HASH_SIZE = 11;
const int STEP = 1;
const int EMPTY = -1;
const int SUCCESS = 1;
const int FAIL = -3;
const int DELETED = -2;
struct Node
{
int value;
}hTbl[HASH_SIZE];
Node data[] = { {44}, {13}, {15}, {8}, {21}, {19}, {30} };
int GetKey(int id)
{
return id % HASH_SIZE;
}
void Init(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
hTbl[i].value = EMPTY;
}
}
void PrintHash(void)
{
for (int i = 0; i < HASH_SIZE; i++)
{
printf("[%2d]: ", i);
if (hTbl[i].value != EMPTY)
{
if (hTbl[i].value == DELETED)
{
printf("Deleted..");
}
else {
printf("%d", hTbl[i].value);
}
}
puts("");
}
puts("");
}
int Insert(Node* data)
{
int pos, key;
pos = key = GetKey(data->value);
for (;;)
{
if (hTbl[pos].value == EMPTY || hTbl[pos].value == DELETED)
{
hTbl[pos] = *data;
return pos;
}
pos += STEP;
if (pos == key) // One Cycle을 돌아서 출발위치 다시 도달한 경우
return FAIL; // Hash Table이 가득찬 상태 (FULL)
if (pos >= HASH_SIZE) // 시작위치를 첫번째 인덱스로 설정
pos = 0;
}
}
Node* Search(int value)
{
int pos, key;
pos = key = GetKey(value);
for (;;)
{
if (hTbl[pos].value == value)
return &hTbl[pos];
if (hTbl[pos].value == EMPTY)
return (Node*)0; // 찾지 못한 경우
pos += STEP;
if (pos == key)
return (Node*)0;
if (pos >= HASH_SIZE)
pos = 0;
}
}
int Remove(int id)
{
Node *p = Search(id);
if (p == (Node*)0)
return FAIL; // 원소를 찾지 못한 경우
p->value = DELETED;
return SUCCESS;
}
void main(void)
{
Init();
for (int i = 0; i < MAX_N; i++)
{
Insert(&data[i]);
}
PrintHash();
int target = 19;
if (Node* p = Search(target))
{
printf("탐색 결과 %d 는 존재.\n", p->value);
}
else
{
printf("탐색 결과 존재하지 않습니다.\n", target);
}
printf("\n=== 삭제 후 상태===\n");
if (Remove(19))
{
PrintHash();
}
if (Node* p = Search(target))
{
printf("탐색 결과 %d 는 존재.\n", p->value);
}
else
{
printf("%d를 탐색 결과 존재하지 않습니다.\n\n", target);
}
}
Reference

'자료구조' 카테고리의 다른 글
| [List] 순차 리스트(정적 배열) & 연결 리스트(동적할당) 비교 (0) | 2021.05.02 |
|---|---|
| [스택] Stack (동적할당, 연결리스트 구현) (0) | 2021.05.02 |
| [해시] Hash Chaining 기법 구현 (0) | 2021.05.01 |
| [해시] Hash란? (2) | 2021.04.30 |
| [큐] 원형 큐 (Circular Queue) (0) | 2021.04.24 |





댓글