출처: [SWEA] SW 문제해결 심화 - 이산수학
Input
3
1 30
100 200
1000 2000
Output
#1 278
#2 9228
#3 912796
ϕ(1) ~ ϕ(N) 합을 구해야 하므로 ϕ(i)를 하나씩 구해서 합하면 TLE 발생
① 에라토스테네스의 체를 이용해 소수 판단. 소수 (Prime Number) 찾기 - 3
소수 (Prime Number) 찾기 - 3
해당 게시글은 에라토스테네스의 체를 이용해서 소수 찾기를 구현한 게시글입니다. - 소수 (Prime Number) 찾기 - 1 - 소수 (Prime Number) 찾기 - 2 ★ 에라토스테네스의 체의 핵심은 소수의 배수를 제
zoosso.tistory.com
② 소수 여부에 따른 오일러 함수 처리 오일러 피(파이) 함수 ϕ(n)
오일러 피(파이) 함수(Euler's phi function)
오일러 피(파이) 함수 ϕ(n) 1~n까지의 수 중에서 n과 서로소인 수의 갯수 ※ 서로소 관계: 두 수 a, b의 공약수가 1뿐인 두 정수를 의미한다. ϕ(1) = 1 (1은 1과 서로소) ϕ(8) = { 1, 3, 5, 7 } =..
zoosso.tistory.com
▶ 1~50까지의 배열 존재. ϕ(1) = 1

▶ 소수인 2와 2의 배수들에 대한 처리 2r × k → (2-1)2r-1 × k
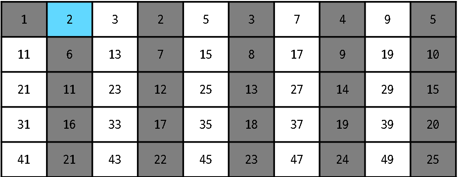
▶ 소수인 3와 3의 배수들에 대한 처리 3r × k → (3-1)3r-1 × k

▶ 소수인 5와 5의 배수들에 대한 처리 5r × k → (5-1)5r-1 × k

▶ 소수인 7와 7의 배수들에 대한 처리 7r × k → (7-1)7r-1 × k

▶ 위의 과정을 50까지의 소수여부에 따라서 동일하게 처리.

③ Phi(1) + phi(2) + … + phi(i) = S[i] = S[i-1] + A[i]
ex) S[10] = S[9] + A[10]

Phi(a) + Phi(a+1) + … + Phi(b) = S[b] - S[a-1]
ex) S[3...6] = S[6] - S[2]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Solution {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int N = 1000000;
// 에라토스테네스의 체를 이용해 소수 판별(= 합성수 여부)
boolean[] isCompositeNumber = new boolean[N+1];
// 합성수도 소수도 아니지만 true
isCompositeNumber[1] = true;
for(int i=2; i*i<=N; i++){
// 에라토스테넷스의 체
if(!isCompositeNumber[i]){
// 배수들을 제외 처리.
for(int j=2; i*j<=N; j++){
isCompositeNumber[i*j] = true;
}
}
}
// 오일러 함수 결과 구하기
int arr[] = new int[N + 1];
for(int i=1; i<=N; i++) {
arr[i] = i;
}
for(int i=2; i<=N; i++) {
// 소수이면
if(!isCompositeNumber[i]){
// 배수들에 대한 처리
for(int j=1; i*j<=N; j++){
arr[i*j] = (i-1) * (arr[i*j] / i);
}
}
}
long[] sum = new long[N+1];
sum[0] = 0; sum[1] = 1;
for(int i=2; i<=N; i++) {
sum[i] = sum[i-1] + arr[i];
}
int T = Integer.parseInt(br.readLine());
for (int tc = 1; tc <= T; tc++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken()); // 정점의 개수
int b = Integer.parseInt(st.nextToken()); // 간선의 개수
long answer = sum[b] - sum[a-1];
System.out.println("#" + tc + " " + answer);
}
}
}
'PS 문제 풀이 > SWEA' 카테고리의 다른 글
| [SWEA] 5642 합 (0) | 2021.02.24 |
|---|---|
| [SWEA] 8016 홀수 피라미드 (0) | 2021.02.24 |
| [SWEA] 8822 홀수 중간값 피라미드 1 (0) | 2021.02.24 |
| [SWEA] 9317 석찬이의 받아쓰기 (0) | 2021.02.24 |
| [SWEA] 3952 줄 세우기 (0) | 2021.02.22 |





댓글