반응형
출처: https://www.acmicpc.net/problem/2805
Binary Search (이분 탐색)
Binary Search (이분 탐색) 정렬된 자료에서 목표값을 찾고자 할 때, 사용되는 탐색기법 O(logN) 리스트 중간의 값(mid)을 선택하여 찾고자 하는 값과 비교하는 방식 분할 정복 알고리즘(Divide and Conquer Al
zoosso.tistory.com
[탐색] Parametric Search
Parametric Search 최적화 문제를 결정 문제로 바꿔 푸는 것 O(logN) ex) Binary Search (이분 탐색)을 이용해서 Lower/Upper Bound를 구하는 경우가 많습니다. Binary Search (이분 탐색) Binary Search (이분 탐..
zoosso.tistory.com
아래와 같이 4개의 나무가 존재할 때 특정 높이(H)로 잘라서 그 윗부분을 상근이가 들고갑니다.
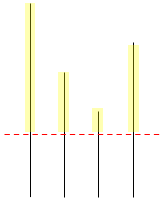
만약 아래와 같이 자른다고 가정했을 때,

필요한 나무보다 많은 양을 가져갈 수는 있지만 낭비되는 부분이 있으며 환경이 좋지 않습니다.
필요한 나무를 구할 수 있는 최적의 높이(높이의 최대값)을 이분탐색을 이용해 구합니다.
(Upper Bound)
#pragma warning (disable : 4996)
#include <stdio.h>
inline int max(int A, int B) { if (A > B) return A; return B;}
const int LM = ((int)1e6 + 10);
int N, need;
int treeHeight[LM];
void input() {
scanf("%d %d", &N, &need);
for (int i = 0; i < N; ++i) {
scanf("%d", treeHeight + i);
}
}
int isPossible(int m) {
int sum = need;
for (int i = 0; i < N; i++) {
// 자르는 높이 > 나무 높이인 경우
if (treeHeight[i] <= m)
continue;
sum -= treeHeight[i] - m;
// 필요한 길이를 만족
if (sum <= 0) return 1;
}
return 0;
}
int solve() {
int start = 0, end = 0, mid, sol = 0;
for (int i = 0; i < N; i++) {
// 제일 나무 높이가 자르는 높이의 최대로 초기 설정
end = max(end, treeHeight[i]);
}
while (start <= end) {//upper bound찾기 (제한 높이가 낮을수록 더 많은 나무를 얻을수 있음)
mid = (start + end) / 2;
if (isPossible(mid)) {
sol = mid; start = mid + 1;
}
else end = mid - 1;
}
return sol;
}
int main() {
input();
printf("%d\n", solve());
}
반응형
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 13458 시험감독 (0) | 2021.02.20 |
|---|---|
| [BOJ] 백준 2531 회전초밥 (0) | 2021.02.20 |
| [BOJ] 백준 6549 히스토그램에서 가장 큰 직사각형 (0) | 2021.02.20 |
| [BOJ] 백준 2571 색종이 - 3 (2) | 2021.02.20 |
| [BOJ] 백준 5639 이진 검색 트리 (0) | 2021.02.20 |





댓글