출처: https://www.acmicpc.net/problem/6549
참고 내용: https://www.acmicpc.net/blog/view/12
Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
Output
8
4000
히스토그램 특징을 이용하는 문제
[BOJ] 백준 2571 색종이 - 3
출처: https://www.acmicpc.net/problem/2571 Input 3 3 7 15 7 5 2 Output 120 완전 탐색방법으로 6중 for문을 이용할 수 있습니다. ① board[][] 배열에 『1』 로 표시된 모든 지점을 찾습니다. ② 찾은..
zoosso.tistory.com
이 문제에서 동일한 방식을 적용했을 경우 O(N2)으로 TLE 발생
[스택] Stack 이란?
Stack 이란? 스택 (Stack) 특징을 가장 잘 나타내는 표현은 후입선출(Last In First Out, LIFO) 이다. ▶ 스택(Stack)은 삽입(push)과 삭제(pop)이 한쪽 끝에서만 일어나는 구조 가장 상단에 위치한 원소를 가리.
zoosso.tistory.com
▶ 스택(Stack)을 이용한 풀이
현재 기둥 높이로 만들 수 있는 직사각형의 정보만 Stack에 저장
push할 때는 마지막 pop한 위치에 현재 기둥 높이로 push
Stack에 들어가는 Data = ([들어가는 위치], 높이)

① [0] 번 막대 (높이 = 2)
스택이 비워져 있으므로 0번 막대 push
→ Stack = ([0], 2)
② [1] 번 막대 (높이 = 1)
[1]번 막대와 스택의 top에 있는 [0]번 막대의 높이 비교
→ 2 > 1 이므로 pop해서 그릴 수있는 직사각형의 넓이를 구합니다.
(top에 있는 것보다 높이가 작아지므로 pop해서 현재 그릴 수 있는 사각형을 구하는 것입니다.)
[1]번 막대가 들어와서 [0]번 막대가 pop 되기 때문에 width = [1] - [0], height = 2
넓이(area) = 1 × 2 = 2

→ [1]막대가 들어가지만 마지막에 pop해서 없어진 [0]번 자리로 들어갑니다. → Stack = ([0], 1)
③ [2]번 막대 (높이 = 4)
→ 스택 top에 있는 막대 높이와 비교 → 1 < 4 이므로 pop 없이 push
→ Stack = ([0], 1) ([2], 4)
④ [3]번 막대 (높이 = 5)
→ 스택 top에 있는 막대 높이와 비교 → 4 < 5 이므로 pop 없이 push
→ Stack = ([0], 1) ([2], 4) ([3], 5)
⑤ [4]번 막대 (높이 = 1)
→ 스택 top에 있는 막대 높이와 비교 → 5 > 1 이므로 pop
width = [4] - [3] = 1 , height = 5 → 넓이 = 1 × 5 = 5

→ Stack = ([0], 1) ([2], 4)
→ 스택 top에 있는 막대 높이와 비교 → 4 > 1 이므로 pop
width = [4] - [2] = 2 , height = 4 → 넓이 = 2 × 4 = 8
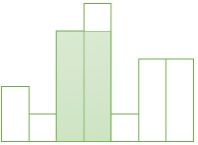
→ Stack = ([0], 1)
→ 스택 top에 있는 막대 높이와 비교 → 1 ≥ 1 이므로 pop
width = [4] - [1] = 3 , height = 1 → 넓이 = 3 × 1 = 3
→ [4]번 막대는 마지막에 pop되었던 [0]의 위치로 push 됩니다. → Stack = ([0], 1)
⑥ [5]번 막대 (높이 = 3)
→ 스택 top에 있는 막대 높이와 비교 → 1 < 3 이므로 pop 없이 push
→ Stack = ([0], 1) ([5], 3)
⑦ [6]번 막대 (높이 = 3)
→ 스택 top에 있는 막대 높이와 비교 → 3 ≥ 3 이므로 pop
width = [6] - [5] = 1 , height = 3 → 넓이 = 1 × 3 = 3

→ Stack = ([0], 1)
→ 스택 top에 있는 막대 높이와 비교 → 1 < 3 이므로 pop없이 push
→ [6]번 막대는 마지막에 pop되었던 [5]의 위치로 push 됩니다.
→ Stack = ([0], 1) ([5], 3)
▶히스토그램을 순회가 끝나면 주어지는 Input Data에 따라 비워지는 경우도 있지만
그렇지 않은 경우도 있기 때문에 Stack이 비워질 때까지 pop 합니다.
이때, top 막대의 위치와 N까지를 width로 해서 면적을 계산합니다.
→ Stack = ([0], 1) ([5], 3)
→ 스택 top에 있는 막대 → width = 7 - 5 = 2 , height = 3 → area = 2 × 3 = 6

→ Stack = ([0], 1) ([5], 3)
→ 스택 top에 있는 막대 → width = 7 - 0 = 7 , height = 1 → area = 7 × 1 = 7
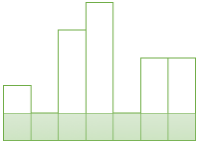
▶ 최대 면적은 면적이 구해질 때마다 최대값을 갱신해서 구합니다.
#pragma warning (disable : 4996)
#include <stdio.h>
typedef long long LL;
inline LL max(LL A, LL B) { if (A > B) return A; return B; }
const int LM = (int)1e5 + 10;
int N, H[LM];
struct Stack {
int idx, height;
};
struct Stack stack[LM];
int sp;
void init() { sp = 0; }
void push(int h, int idx) {
stack[++sp].height = h;
stack[sp].idx = idx;
}
void pop() { sp--; }
struct Stack top() { return stack[sp]; }
int empty() { return sp == 0; }
int size() { return sp; }
void input() {
scanf("%d", &N);
if (N == 0) return;
for (int i = 0; i < N; i++)
scanf("%d", H + i);
}
LL solve() {
LL ans = 0, area;
for (int i = 0; i < N; i++) {
int pos = i;
while (!empty() && (top().height >= H[i])) {
pos = top().idx;
area = (LL)top().height * (i - pos);
ans = max(ans, area);
pop();
}
push(H[i], pos);
}
while (!empty()) {
area = (LL)top().height * (N - top().idx);
ans = max(ans, area);
pop();
}
return ans;
}
int main() {
// freopen("input.txt", "r", stdin);
for (;;) {
input();
if (N == 0) break;
printf("%lld\n", solve());
}
}순회가 끝나고 스택이 비워지지 않는 경우를 대비해서
높이 = 0인 data가 마지막에 한 개 더 있도록 설계할 수도 있습니다.
LL solve() {
H[N] = 0; // 마지막에 스택을 전부 비워주기 위함
LL ans = 0, area;
for (int i = 0; i <= N; i++) {
int pos = i;
while (!empty() && (top().height >= H[i])) {
pos = top().idx;
area = (LL)top().height * (i - pos);
ans = max(ans, area);
pop();
}
push(H[i], pos);
}
return ans;
}
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 2531 회전초밥 (0) | 2021.02.20 |
|---|---|
| [BOJ] 백준 2805 나무 자르기 (0) | 2021.02.20 |
| [BOJ] 백준 2571 색종이 - 3 (2) | 2021.02.20 |
| [BOJ] 백준 5639 이진 검색 트리 (0) | 2021.02.20 |
| [BOJ] 백준 8983 사냥꾼 (0) | 2021.02.20 |





댓글