Merge Sort
분할 정복(divide and conquer) 기법으로 만들어진 정렬 방법 → O(N * logN)
- 1단계 분할(Divide) - 해결이 용이한 단계까지 문제를 분할해 나간다.
- 2단계 정복(Conquer) - 해결이 용이한 수준까지 분할된 문제를 해결한다.
- 3단계 결합(Combine) - 분할해서 해결한 결과를 결합하여 마무리한다.
※ 일반적으로 정렬할 자료의 양이 많으면 많을수록 정렬 수행시간은 기하급수적으로 길어져
많은 자룔르 한번 정렬하는 것 보다 적은 수의 자료를 여러 번 정렬 하는 것이 유리하다고 판단합니다.
ex) { 6, 5, 3, 1, 8, 7, 2, 4 }를 병합정렬 하는 과정

시뮬레이션

[분할 과정]
재귀함수르 통해 크기가 = 1 (left >= right)될 때까지 분할 합니다.

[merge 과정]
작은 단위부터 merge할 때, 오름차순에 맞게 자리를 찾아갑니다.

병합 정렬을 구현할 때, 정렬에 사용되는 배열 변수를 '전역 변수'로 선언해야 공간복잡도가 효율적입니다.
재귀 함수 과정에서 새롭게 배열을 생성하면 메모리 낭비가 큽니다.
① x, y 비교 ▶ 4 < 3 이므로 k 위치에 3을 넣습니다. (y++, k++)

② 4 < 5 이므로 k 위치에 4를 넣습니다. (x++, k++)
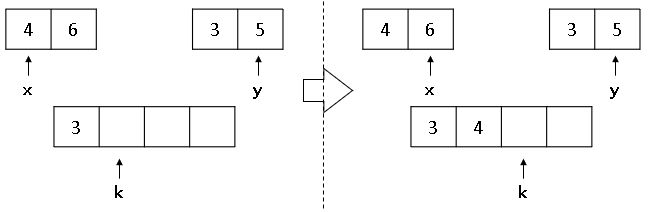
③ 6 > 5 이므로, k 위치에 5를 넣습니다. (y++, k++)

④ 우측에는 더 이상 비교할 대상이 없으므로 좌측의 모든 숫자를 아래 배열에 채웁니다.

[또 다른 예시]
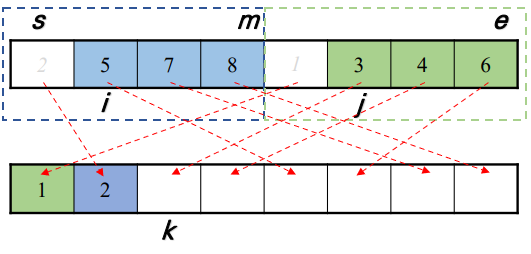
▶ 시간 복잡도 O(N logN)
퀵 정렬은 Pivot 값에 따라서 편향되게 분할할 가능성이 있다는 점에서
최악의 경우 O(N2)의 시간 복잡도가 날 수 있지만,
병합 정렬은 분할과정이기 때문에 원소의 배치와 상관없이 O(N * logN)을 보장합니다.
# include <stdio.h>
int sorted[10];
void merge(int arr[], int left, int mid, int right) {
int x = left, y = mid + 1;
int k = left;
/* 분할 정렬된 arr의 합병 */
while (x <= mid && y <= right) {
if (arr[x] <= arr[y])
sorted[k++] = arr[x++];
else
sorted[k++] = arr[y++];
}
// 우측에 남아있는 원소를 일괄 복사
if (x > mid) {
for (int i = y; i <= right; i++)
sorted[k++] = arr[i];
}
// 좌측에 남아있는 원소를 일괄 복사
else {
for (int i = x; i <= mid; i++)
sorted[k++] = arr[i];
}
// 배열 sorted[](임시 배열)의 원소를 배열 arr[]로 재복사
for (int i = left; i <= right; i++) {
arr[i] = sorted[i];
}
}
// 합병 정렬
void mergeSort(int arr[], int left, int right) {
if (left >= right) return;
int mid = (left + right) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
void main() {
int n = 10;
int arr[10] = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };
mergeSort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
}
Reference
- [Jungol] 3519 Tutorial : 합병(병합)정렬(Merge Sort)
- [BOJ] 10090 Counting Inversions

'알고리즘' 카테고리의 다른 글
| [탐색] Parametric Search (0) | 2021.03.04 |
|---|---|
| PS시 어떤 정렬을 선택하는 것이 좋을까? (0) | 2021.03.02 |
| 연속된 부분 합(연속합) - 2 (Prefix Sum) (0) | 2021.02.28 |
| 연속된 부분 합(연속합) - 3 (DP) (0) | 2021.02.28 |
| 알고리즘 문제에서 시간 복잡도는 어떻게 하는걸까? (빅-오) (0) | 2021.02.28 |





댓글