출처: https://algospot.com/judge/problem/read/CHRISTMAS
Input
1
6 4
1 2 3 4 5 6
Output
3 1
[1] 한 번 주문할 수 있다면, 가능한 주문 방법은 몇 가지인가?
K = 4, (1 2 3 4 5 6) 배열에서 [2, 4]구간 선택
3 + 4 + 5 = 12로 4명의 아이에게 3개씩 나누어 주면됩니다.
즉, 특정 구간의 합이 K로 나누어떨어지면 됩니다. ← 나머지 연산(modulo)
① [H, T] 구간의 합 = (psum[T] - psum[H - 1])
② 해당 구간의 합이 K명의 아이들에게 나눠줄 수 있는 경우
(psum[T] - psum[H - 1]) mod K = 0
③ (나머지 연산 적용 후) psum[T] mod K = psum[H - 1] mod K
즉, 부분합 배열인 psum[i] = i번까지의 부분합 % K를 저장합니다.
※ psum[0] = 0 으로 설정 → (Test Case) psum = [0 1 3 2 2 3 1]
④ 경우의 수 구하기 count[] 배열을 생성하여 pusm[i]가 등장한 횟수를 저장 (like 계수 정렬)
count[pusm[i]]++ 적용; psum = [0 1 3 2 2 3 1] → count = [1 2 2 2]
⑤ 전체 경우의 수는 count[] 값 ≥ 2에 해당되는 곳에서 2가지 경우를 뽑는 것입니다.
(Test Case) 2C2 + 2C2 + 2C2 = 3
ex) count = [1 3 4 2] → 3C2 + 4C2 + 2C2 = 3 + 6 + 1 = 10
가령, psum[i] = 3이 나오는 지점이 3개(= count[3])라고 했을 때, → (x, y, z)
구간을 선택하는 경우의 수는 [x, y], [x, z], [y, z]로 3C2이기 때문입니다.
[2] 주문이 겹치지 않게 최대 몇 번 주문하는 경우의 수는 부분합과 DP 이용
DP[i] = 0번 상자부터 i번 상자까지 서로 겹치지 않고 구매할 수 있는 최대 수
DP[i] = max(i 번째 상자를 선택하지 않는 경우, i 번째 상자를 선택하는 경우)
= max(DP[i-1], DP[최근에 psum값이 같았던 인덱스] + 1)
= max(DP[i-1], DP[prev[psum[i]]] + 1)
※ prev[s] = 이전에 psum[] 값이 s였던 마지막 위치
i 번째를 상자를 주문한 경우, psum[i] 값을 이전에도 본 적이 있는지 확인.
동적계획법(Dynamic Programming, DP)
동적계획법(Dynamic Programming, DP)
동적 계획법(Dynamic Programming)은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다. 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한
zoosso.tistory.com
시뮬레이션
DP[]의 모든 값을 0으로 초기화
prev[0] = 0, 나머지는 prev[ ] 값 = -1 초기화
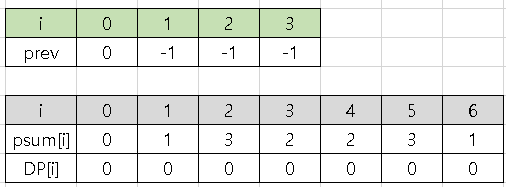
prev[1] = -1이므로, DP[1] = DP[1-1] = 0
prev[psum[1]] = prev[1] = 1
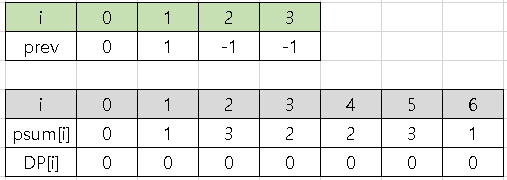
prev[3] = -1이므로, DP[2] = DP[2-1] = 0
prev[psum[2]] = prev[3] = 2

prev[2] = -1이므로, DP[3] = DP[3-1] = 0
prev[psum[3]] = prev[2] = 3

DP[4] = max(DP[3] + DP[prev[psum[4]]] + 1) = max(DP[3] + DP[prev[2]] + 1)
즉, prev[2]는 현재 psum[4]값이 나타난 최근(마지막) 위치를 나타냅니다.
= max(DP[3], DP[3] + 1) = max(0, 1) = 1
prev[2] = 4가 됩니다.

DP[5] = max(DP[4], DP[2] + 1) = 1
prev[3] = 5

DP[6] = max(DP[5], DP[1] + 1) = 1
prev[1] = 6

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;
int waysToBuy(const vector<int>& psum, int K) {
const int MOD = 20091101;
int result = 0;
//psum[]의 각 값을 몇 번이나 본 적 있는지 기록
vector<long long> count(K, 0);
for (int i = 0; i < psum.size(); i++) {
count[psum[i]]++;
}
// 두 번 이상 본 적 있다면 이 값 중 두 개를 선택하는 방법의 수를 더한다
// 즉, count[i]개 중 2개를 고를 경우의 수 (조합 공식 이용)
for (int i = 0; i < K; i++)
if (count[i] >= 2)
result = (result + ((count[i] * (count[i] - 1)) / 2)) % MOD;
return result;
}
int maxBuys(const vector<int>& psum, int K) {
vector<int> dp(psum.size(), 0);
vector<int> prev(K, -1);
for (int i = 0; i < psum.size(); i++) {
//i번째 상자를 아예 고려하지 않는 경우
if (i > 0)
dp[i] = dp[i - 1];
else
dp[i] = 0;
// psum[i]를 전에도 본 적이 있다면, prev[psum[i]]+1부터 여기까지 전부 구매
int loc = prev[psum[i]];
if (loc != -1) {
// i 번째 상자를 산 경우와 사지 않은 경우
dp[i] = max(dp[i], dp[loc] + 1);
}
//prev[]에 현재 위치 기록
prev[psum[i]] = i;
}
return dp.back();
}
int main(void) {
int C;
cin >> C;
while (C--) {
int N, K;
cin >> N >> K;
vector<int> v(N);
for (int i = 0; i < N; i++) {
cin >> v[i];
}
vector<int> psum(N + 1);
psum[0] = 0;
// 어린이들에게 인형을 모두 나눠주려면 인형의 총 수가 K의 배수여야하므로
// 부분합 구하기 (K로 나눈 나머지로 값 저장)
for (int i = 1; i <= N; i++) {
psum[i] = (psum[i - 1] + v[i - 1]) % K;
}
cout << waysToBuy(psum, K) << " " << maxBuys(psum, K) << endl;
}
}
'PS 문제 풀이 > Algospot' 카테고리의 다른 글
| [Algospot] 알고스팟 TRAVERSAL 트리 순회 순서 변경 (0) | 2021.03.01 |
|---|---|
| [Algospot] 알고스팟 ITES 외계 신호 분석 (0) | 2021.03.01 |
| [Algospot] 알고스팟 PICNIC 소풍 (0) | 2021.03.01 |
| [Algospot] 알고스팟 JUMPGAME 외발 뛰기 (0) | 2021.03.01 |
| [Algospot] 알고스팟 BRACKETS2 짝이 맞지 않는 괄호 (0) | 2021.03.01 |





댓글