출처: https://algospot.com/judge/problem/read/JUMPGAME
Input
2
7
2 5 1 6 1 4 1
6 1 1 2 2 9 3
7 2 3 2 1 3 1
1 1 3 1 7 1 2
4 1 2 3 4 1 2
3 3 1 2 3 4 1
1 5 2 9 4 7 0
7
2 5 1 6 1 4 1
6 1 1 2 2 9 3
7 2 3 2 1 3 1
1 1 3 1 7 1 2
4 1 2 3 4 1 3
3 3 1 2 3 4 1
1 5 2 9 4 7 0
Output
YES
NO
▶ 동적계획법(Dynamic Programming, DP)
동적계획법(Dynamic Programming, DP)
동적 계획법(Dynamic Programming)은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다. 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한
zoosso.tistory.com
그림과 같이 N × N 크기의 격자에 각 1부터 9 사이의 정수가 존재.
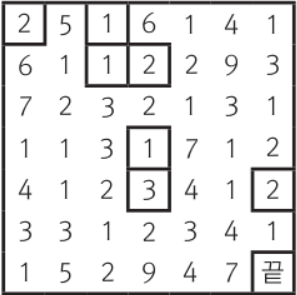
- 맨 왼쪽 윗 칸에서 출발하여 오른쪽 아래 칸으로 이동하여 『끝』 지점까지 이동
이동할 때, 각 칸에 적혀 있는 숫자만틈 이동 가능
- 중간에 게임판을 벗어날 수 없습니다.
- 경우에 따라서는 『끝』 지점에 도착할 수 없을 수 있습니다.

Test Case 개수와 게임판의 크기 N이 주어질 때, (1 ≤ N ≤ 100)
왼쪽 위 시작점에서 오른쪽 아래 끝 지점까지 도달할 수 있는 방법이 있는지 출력
재귀 호출
동적 계획법 알고리즘을 만드는 첫 단계는 해당 문제를
재귀적으로 해결하는 완전 탐색 알고리즘을 만드는 것
▶ 완전 탐색으로 구현하는 경우 TLE 발생
import java.util.Scanner;
public class Main{
static int n;
static int[][] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Test Case 개수
int C = Integer.parseInt(sc.next());
for(int i=0; i<C; i++) {
n = Integer.parseInt(sc.next());
arr = new int[n+1][n+1];
// 격자 입력 받기
for(int x=1; x<=n; x++) {
for(int y=1; y<=n; y++) {
arr[x][y] = Integer.parseInt(sc.next());
}
}
if(jump(1,1)) {
System.out.println("YES");
}else {
System.out.println("NO");
}
}
}
private static boolean jump(int x, int y) {
// 배열 범위를 초과하지 않는 선에서
if(x<1 || y<1) return false;
if(x>n || y>n) return false;
// 정확히 끝지점에 도달했다면
if(x == n && y == n) return true;
// 오른쪽 방향이든 아래방향이든 재귀함수를 통해 어떤 경로였든 도착했다면 true
return jump(x+arr[x][y], y) || jump(x, y+arr[x][y]);
}
}1
7
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 2
1 1 1 1 1 2 끝
'끝' 지점에 '2'가 있기때문에 어떤 경로이든 끝에 도달할 수 없습니다.
격자의 크기 N이 늘어남에 따라 시간 복잡도는 지수적으로 증가.
메모이제이션을 적용해서 중복된 연산을 없앨 수 있다.
▶ 특정 격자에서 두번 이상 탐색할 필요없이
해당 격자에서 탐색을 이미 했다면 '표시(흔적)'을 남겨두는 것
import java.util.Scanner;
public class Main{
static int n;
static int[][] arr;
static int[][] cache;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Test Case 개수
int C = Integer.parseInt(sc.next());
for(int i=0; i<C; i++) {
n = Integer.parseInt(sc.next());
arr = new int[n+1][n+1];
cache = new int[n+1][n+1];
// 격자 입력 받기
for(int x=1; x<=n; x++) {
for(int y=1; y<=n; y++) {
arr[x][y] = Integer.parseInt(sc.next());
}
}
jump(1,1);
// 도착할 수 있는 격자배열이라면
if(cache[n][n] == 1) {
System.out.println("YES");
}else {
System.out.println("NO");
}
}
}
private static void jump(int x, int y) {
// 배열 범위를 초과하지 않는 선에서
if(x<1 || y<1) return;
if(x>n || y>n) return;
// 정확히 끝지점에 도달했다면
if(x == n && y == n) {
cache[n][n] = 1;
return;
}
// 아직 탐색한적이 없는 격자라면
if(cache[x][y] == 0) {
// 'cache' 탐색 여부를 저장
cache[x][y] = -1;
// 오른쪽 방향으로 탐색 시도
jump(x+arr[x][y], y);
// 아래 방향으로 탐색 시도
jump(x, y+arr[x][y]);
}
}
}
'PS 문제 풀이 > Algospot' 카테고리의 다른 글
| [Algospot] 알고스팟 CHRISTMAS 크리스마스 인형 (0) | 2021.03.01 |
|---|---|
| [Algospot] 알고스팟 PICNIC 소풍 (0) | 2021.03.01 |
| [Algospot] 알고스팟 BRACKETS2 짝이 맞지 않는 괄호 (0) | 2021.03.01 |
| [Algospot] 알고스팟 JOSEPHUS 조세푸스 문제 (0) | 2021.03.01 |
| [Algospot] 알고스팟 LAN 근거리 네트워크 (0) | 2021.03.01 |





댓글