출처: [SWEA] SW 문제해결 심화 - 증명의 중요성
Input
2
5 5
1 2 1
4 3 2
1 3 1
2 4 2
5 4 3
4 4
1 2 1000
2 3 100
3 4 500
1 4 600
Output
#1 7
#2 1700

[1] - [2], [2] - [4], [4] - [5], [1] - [3]
가중치 합: 1 + 2 + 3 + 1 = 7
위의 예제로만 보면 최소 신장 트리를 구성하는 Prim's Algorithm을 적용하면 되지만,
[Test Case #2]
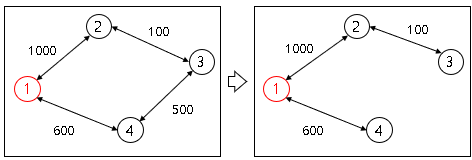
가중치 합: 1000 + 600 + 100 = 1700 입니다.
[정점 [1] 기준 Prim's Algorithm 결과]
이는 최소신장트리 ≠ 최단 경로이기 때문입니다.
최소신장트리에서는 정점[1] → [2]까지 600 + 500 + 100 = 1200 이지만
원형 그래프에서 가중치 1000으로 바로 가는 경로가 존재하기 때문입니다.
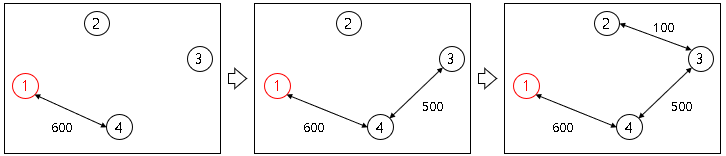
[정점 [1] 기준으로 다익스트라 알고리즘 결과]

정점 [1] → [3] 경로가 [1] - [4] - [3]이 되어, 가중치 합: 1000 + 600 + 500 = 2100 입니다.
이는, [1] → [3]까지 가중치 합 = 1100으로, [1] - [2] - [3] / [1] - [4] - [3] 동일하기 때문입니다.
구현
다익스트라 (Dijkstra)
개념 다익스트라 알고리즘은 Single Source shortest path problem으로 하나의 정점에서 다른 모든 정점까지 최단 경로를 구할 때 주로 사용됩니다. 이때, 간선의 가중치는 only 양수가 전제조건입니다. (
zoosso.tistory.com
일반적인 다익스트라 알고리즘에서는 특정 정점으로 가는 경로가 더 적은 비용일 때 갱신됩니다.
전체 경로(Edge)의 최소 비용을 위해서는 동일한 비용이 드는 경우, 직전 경로 가중치가 더 낮은 간선을 선택합니다.

아래의 경우에는 [1] → [3]으로 가는 경로는 1000 + 100 = 600 + 500 = 1100 동일하지만,
100 < 500 이므로 [1] → [2] → [3]되도록 경로를 수정.

* 정점과 간선의 개수가 많으며, 가중치 값의 범위가 크므로 RunTime Error에 주의
- 인접 리스트 방식의 그래프 표현
- 우선순위 큐를 이용해 다익스트라 구현
- 메모리를 많이 차지하는 변수는 static 할당
- 매 Test Case마다 System.gc()를 이용해 메모리 정리
하나의 테스트 케이스가 종료되어도 기존 할당된 메모리들이
바로 Garbage Collecting 되지 않고 누적되어 발생하는 현상이 있을 수 있음
import java.io.*;
import java.util.*;
public class Solution {
static final long INF = Long.MAX_VALUE;
static final int UNVISITED = -1;
static int N, M;
static long answer;
static long[] dist;
static int[] trace;
static boolean[] visited;
static List<List<Node>> adList; // 인접 리스트
static PriorityQueue<Node> pq;
static class Node implements Comparable<Node> {
int ID;
long cost;
boolean checked;
public Node(int ID, long cost) {
this.ID = ID;
this.cost = cost;
this.checked = false;
}
@Override
public int compareTo(Node target) {
// 작은 거리 비용이 먼저 오도록
if(this.cost - target.cost < 0)
return -1;
return 1;
}
}
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
int T = Integer.parseInt(sc.next());
for (int tc = 1; tc <= T; tc++) {
N = Integer.parseInt(sc.next());
M = Integer.parseInt(sc.next());
adList = new ArrayList<>();
// 인덱스를 1부터 하기 위해 임의로 한 개 넣어둠
adList.add(new<Node> ArrayList());
for(int i=1; i<=N; i++) {
adList.add(new<Node> ArrayList());
}
while(M-- > 0) {
int u = Integer.parseInt((sc.next()));
int v = Integer.parseInt((sc.next()));
long cost = Long.parseLong((sc.next()));
adList.get(u).add(new Node(v, cost));
adList.get(v).add(new Node(u, cost));
}
answer = 0;
pq = new PriorityQueue<>();
visited = new boolean[N+1];
dist = new long[N+1];
trace = new int[N+1];
Arrays.fill(dist, INF); Arrays.fill(trace, UNVISITED);
// 다익스트라 알고리즘
dijkstra(1);
visited = null; dist = null;
trace = null; adList = null;
System.gc();
System.out.println("#" + tc + " " + answer);
}
}
private static void dijkstra(int start) {
dist[start] = 0; trace[start] = start;
pq.add(new Node(start, 0));
while(!pq.isEmpty()) {
Node current = pq.poll();
// 재방문 여부 확인
if(visited[current.ID]) continue;
visited[current.ID] = true;
// 연결된 정점들을 확인
for(Node next : adList.get(current.ID)) {
// 효율적인 처리를 위해 최소 거리 비용이 갱신되는 경우만 queue에 넣어줍니다.
if(dist[next.ID] >= dist[current.ID] + next.cost) {
// 최소 거리 비용 갱신
dist[next.ID] = dist[current.ID] + next.cost;
// 해당 정점(next)을 거치기 위해서는 현재 정점(current)을 직전에 거치도록 표시
// 처음 방문하는 곳인지 확인
if(trace[next.ID] == UNVISITED) {
trace[next.ID] = current.ID;
}
else {
// 재방문인 경우 좀 더 짧은 거리로 도달 했는지 확인
Node A = findEdge(current.ID, next.ID);
Node B = findEdge(trace[next.ID], next.ID);
if(A.cost < B.cost) trace[next.ID] = current.ID;
}
pq.add(new Node(next.ID, dist[next.ID]));
}
}
}
// 경로 추적
tracert(start);
}
// 다익스트라 경로 추적
private static void tracert(int start) {
// start 정점에서 각 정점[v]까지 최단 경로 추적
for(int v = 1; v <= N; v++) {
// 자기 자신인 경우
if(v == start) {
continue;
}
int prev;
for(prev = v; prev != start; prev = trace[prev]) {
int A = prev;
int B = trace[prev];
Node edge = findEdge(A, B);
// 해당 간선이 아직 청소하지(지나가지) 않았는지 확인
if(edge.checked) {
break;
}
else {
// 가중치를 더해줍니다.
answer += edge.cost;
edge.checked = true;
// 반대방향 간선도 동일하게 표시
Node converseEdge = findEdge(B, A);
converseEdge.checked = true;
}
}
}
}
// A-B edge 찾는 함수
private static Node findEdge(int A, int B) {
Node edge = null;
List<Node> list = adList.get(A);
for(int i=0; i<list.size(); i++) {
edge = list.get(i);
if(edge.ID == B) {
break;
}
}
return edge;
}
}
'PS 문제 풀이 > SWEA' 카테고리의 다른 글
| [SWEA] 1768 숫자야구게임 (0) | 2021.02.27 |
|---|---|
| [SWEA] 4006 고속도로 건설 2 (0) | 2021.02.27 |
| [SWEA] 4007 간담회 참석 (0) | 2021.02.25 |
| [SWEA] 4066 All Pair Shortest Path (0) | 2021.02.25 |
| [SWEA] 3260 두 수의 덧셈 (0) | 2021.02.24 |





댓글