Input
1
4 1
1 2
2 3
3 2
4 -1
Output
#1 2
A1 = 1, A2 = 1, An = An-1 + An-2 (n ≥ 3)
피보나치 수열을 구현하는 방법 중 2가지가 있습니다.
▶ 동적계획법(Dynamic Programming, DP)
동적계획법(Dynamic Programming, DP)
동적 계획법(Dynamic Programming)은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다. 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한
zoosso.tistory.com
구현
▶ DP[i] = i 번째 점을 포함하며 그 점까지 조건을 만족하는 꺽은 선 중 선분 개수의 최솟값
현재 점(i)에서 뒤르 보며 해당 점(j)가 가능한 기울기의 범위 내에 있는 경우
D[j]를 D[i] + 1로 갱신여부 확인 후 변경
재귀 + 메모이제이션를 이용한 방식
int A[] = new int[n+1];
A[1] = 1; A[2] = 1;
int fibo(int n){
if(A[n] != 0) return A[n];
return A[n] = fibo(n-1) + fibo(n-2);
}
DP를 이용한 방식
- A[i] 입장에서는 A[i-1], A[i-2] 값을 당겨서 가져오는 관점
int A[] = new int[n+1];
A[1] = 1; A[2] = 1;
for(int i=3; i<=n; i++){
A[i] = A[i-1] + A[i + 1]
}
DP를 이용한 방식
- A[i] 입장에서 A[i-1], A[i-2]가 밀어준 값을 사용하는 관점
int A[] = new int[n+1];
A[1] = 1; A[2] = 1;
for(int i=1; i<=n-2; i++){
A[i + 1] += A[i]
A[i + 2] += A[i]
}
Test Case 시뮬레이션
- 주황색 선분 : 가능한 가장 큰 기울기
- 빨간색 선분 : 가능한 가장 작은 기울기

DP[1] = 0을 제외하고 나머지 DP[]는 무한대로 초기화
첫번째 좌표를 기준점으로 설정(pivot)

(2)번 점은 U, L 사이에 존재
∞ > DP[1] + 1 이므로 DP[2] = 1

U 기울기 감소
(3)번 점은 U, L 사이에 존재 (정확히는 L 선분 위에 존재)
∞ > DP[1] + 1 이므로 DP[3] = 1
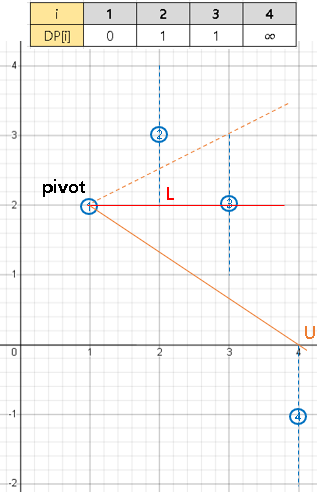
U 기울기 감소
선분 L > 선분 U 이므로 탐색 종료

(3)점은 U와 L 사이에 있으므로 갱신 시도
1 < DP[2] + 1 이므로 값 변경 X

U 기울기 감소
(4)번 점은 U, L 사이에 존재 (정확히는 L 선분 위에 존재)
∞ > DP[2] + 1 이므로 DP[4] = 2로 변경
더 이상 탐색할 점이 없으므로 종료.

(4)번 점은 U, L 사이에 존재
But, 2 = DP[3] + 1 이므로 값 변경 X
더 이상 탐색할 점이 없으므로 종료.
※ DP를 구현할 때는 아래와 같이 관점의 차이를 둘 수 있음
현재 점(i)에서 뒤를 보며
해당 점(j)이 가능한 기울기의 범위 내에 있는 경우
D[ j ]를 D[ i ]+1으로 갱신 시도
현재 점(i)에서 역순으로 앞을 보며
해당 점(j)이 가능한 기울기의 범위 내에 있는 경우
D[ i ]를 D[ j ]+1으로 갱신 시도
import java.io.*;
import java.util.*;
public class Solution {
static final long INF = Long.MAX_VALUE;
static int N;
static long epsilon;
static Point[] points;
static Long[] DP;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
int T = Integer.parseInt(br.readLine());
for (int tc = 1; tc <= T; tc++) {
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
epsilon = Long.parseLong(st.nextToken());
points = new Point[N];
for(int i=0; i<N; i++) {
st = new StringTokenizer(br.readLine());
long x = Long.parseLong(st.nextToken());
long y = Long.parseLong(st.nextToken());
points[i] = new Point(x, y);
}
// (1차) x좌표 기준 오름차순
// (2차) y좌표 기준 오름차순
Arrays.sort(points);
DP = new Long[N];
Arrays.fill(DP, INF);
DP[0] = 0L;
for(int i=0; i<N-1; i++) {
Point pivot = points[i];
Point U = new Point(points[i+1].x, points[i+1].y + epsilon);
Point L = new Point(points[i+1].x, points[i+1].y - epsilon);
if(DP[i+1] > DP[i]) DP[i+1] = DP[i] + 1;
for(int j=i+2; j<N; j++) {
// 기울기 범위 조정 (동일선상의 경우, 기존 U과 L 변경 불필요)
// 반시계 방향으로, 최대 기울기 감소
Point tempU = new Point(points[j].x, points[j].y + epsilon);
if(ccw(pivot, U, tempU) < 0) {
U = tempU;
}
// 시계 방향으로, 최소 기울기 감소
Point tempL = new Point(points[j].x, points[j].y - epsilon);
if(ccw(pivot, L, tempL) > 0) {
L = tempL;
}
if(ccw(pivot, U, L) > 0) {
break;
}
// 최소 기울기 선분보다 위에, 최대 기울기 선분보다 아래에 존재하는지 확인
// 최소 기울기 선분과 시계 방향이거나 동일선상에 존재 필요
// 최대 기울기 선분과 반시계 방향이거나 동일선상에 존재 필요
if(ccw(pivot, L , points[j]) >= 0 && ccw(pivot, U , points[j]) <= 0) {
// 기존 값이(DP[j]) DP[i]+1 보다 더 큰 경우에만 변경
if(DP[j] > DP[i] + 1) {
DP[j] = DP[i] + 1;
}
}
}
}
System.out.println("#" + tc + " " + DP[N-1]);
}
}
// 벡터의 외적을 이용한 ccw 확인
private static int ccw(Point p, Point q, Point r) {
// 점 p, q에대해 점 r의 x, y를 빼줘서 그래프를 원점에 맞춥니다.
long result = ((q.x - p.x) * (r.y - p.y)) - ((q.y - p.y) * (r.x - p.x));
if (result > 0)
// 시계 반향
return 1;
else if (result < 0)
// 반시계
return -1;
else
// 일직선
return 0;
}
}
class Point implements Comparable<Point>{
long x, y;
public Point(long x, long y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point target) {
if(this.x - target.x < 0)
return -1;
else if(this.x - target.x > 0)
return 1;
else { // x 좌표가 같은 경우
if(this.y - target.y < 0) return -1;
else return 1;
}
}
}
'PS 문제 풀이 > SWEA' 카테고리의 다른 글
| [SWEA] 4042 Closest (0) | 2021.03.01 |
|---|---|
| [SWEA] 4052 프리랜서 (0) | 2021.03.01 |
| [SWEA] 3950 괄호 (0) | 2021.03.01 |
| [SWEA] 4039 두 번 이상 등장하는 문자열 (0) | 2021.03.01 |
| [SWEA] 4040 문자열의 거듭제곱 (0) | 2021.03.01 |





댓글