출처: https://algospot.com/judge/problem/read/INSERTION
Input
2
5
0 1 1 2 3
4
0 1 2 3
Output
5 1 4 3 2
4 3 2 1
뒤에서 부터 문제를 풀어 나갑니다.
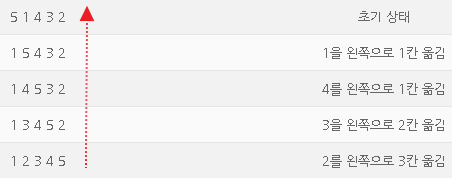
① [1 3 4 5 2]에서 2를 왼쪽으로 3칸 옮겨서 [1 2 3 4 5]가 만들어 졌으므로
2를 다시 오른쪽으로 3칸 움직이면 됩니다.
즉, 2보다 큰 숫자가 3개 존재하고 있었습니다.
A[N-1] = 2
① [1 3 4 5]는 [1 4 5 3]에서 3을 왼쪽으로 2칸으로 옮긴 것이므로
3을 다시 오른쪽으로 움직이면 A[N-2] = 3
② [1 4 5]는 [1 5 4]에서 4를 왼쪽으로 1칸 옮긴 것이므로
4를 오른쪽으로 한칸 이동합니다 A[N-3] = 4
③ [1 5]는 [5 1]에서 1을 왼쪽으로 1칸 옮긴 것이므로
1을 오른쪽으로 한칸 이동합니다. A[N-4] = 1
④ 초기 상태이므로 A[N-5] = A[0] = 5
배열 원소값을 이진 탐색 트리 구조로 저장하기 위해서는 보통, STL의 set, map을 사용하지만
k 번째 원소를 찾는 기능을 제공하지 않기 때문에 직접 구현한 자료구조 트립(Treap) 사용
※ Treap
Tree + Heap인 자료 구조
기존 이진 트리는 어떻게 내가 삽입(insert)하느냐에 따라서
트리의 높이가 O(N)이 될 수 있고 O(logN)이 될수도 있는 문제점이 있다.
트리구조의 기본적인 목표는 최대한 높이를 낮추어 탐색의 시간을 빠르게 하는 것이 목적인데
높이가 O(N)되면 선형 구조와 다를바가 없어진다. 즉, 균형의 문제가 발생
균형의 문제를 해결하기위한 자료구조로는 AVL Tree와 Red Black Tree가 있는데 이것들은 구현하기가 어렵다.
그래서 간단히 Heap의 성질을 이용해서 구현한것이 Treap이다
#include <iostream>
#include <ctime>
#include <cstdlib>
using namespace std;
struct Node {
int key;
int priority;
int size; // 이 노드를 루트로 하는 서브트리 크기
Node* left, *right;
Node(const int& _key) : key(_key), priority(rand()), size(1), left(NULL), right(NULL) {}
void setLeft(Node* newLeft) { left = newLeft; calcSize(); }
void setRight(Node* newRight) { right = newRight; calcSize(); }
void calcSize() {
size = 1;
if (left) size += left->size;
if (right) size += right->size;
}
};
typedef pair<Node*, Node*> NodePair;
// root를 루트로 하는 트립을 key값과 비교하여 두 개의 트립으로 분리
NodePair split(Node* root, int key) {
if (root == NULL)
return NodePair(NULL, NULL);
// 루트가 key 미만이면 오른쪽 서브트리를 split
if (root->key < key) {
NodePair rs = split(root->right, key);
root->setRight(rs.first);
return NodePair(root, rs.second);
}
// 루트가 key 이상이면 왼쪽 서브트리를 split
else {
NodePair ls = split(root->left, key);
root->setLeft(ls.second);
return NodePair(ls.first, root);
}
}
// root를 루트로 하는 트립에 새 node를 삽입하여 결과 트립의 루트 반환
Node* insert(Node* root, Node* node) {
if (root == NULL) return node;
if (root->priority < node->priority) {
NodePair splitted = split(root, node->key);
node->setLeft(splitted.first);
node->setRight(splitted.second);
return node;
}
else if (node->key < root->key) {
root->setLeft(insert(root->left, node));
}
else
root->setRight(insert(root->right, node));
return root;
}
// a와 b가 두 개의 트립이고 max(a)<min(b)일 때 이 둘을 합친다
Node* merge(Node* a, Node* b) {
if (a == NULL) return b;
if (b == NULL) return a;
if (a->priority < b->priority) {
b->setLeft(merge(a, b->left));
return b;
}
else {
a->setRight(merge(a->right, b));
return a;
}
}
// root를 루트로 하는 트립에서 key를 지우고 결과 트립의 루트 반환
Node* erase(Node* root, int key) {
if (root == NULL) return root;
if (root->key == key) {
Node* ret = merge(root->left, root->right);
delete root;
return ret;
}
if (key < root->key)
root->setLeft(erase(root->left, key));
else
root->setRight(erase(root->right, key));
return root;
}
// root를 루트로 하는 트리 중에서 k번째 원소 반환
Node* kth(Node* root, int k) {
int leftSize = 0;
if (root->left != NULL) leftSize = root->left->size;
if (k <= leftSize) return kth(root->left, k);
if (k == leftSize + 1) return root;
return kth(root->right, k - leftSize - 1);
}
// key보다 작은 키 값의 수 반환
int countLessThan(Node* root, int key)
{
if (root == NULL)
return 0;
if (root->key >= key)
return countLessThan(root->left, key);
int ls = (root->left ? root->left->size : 0);
return ls + 1 + countLessThan(root->right, key);
}
int C, N, A[50001], shifted[50001];
void solve() {
Node* candidate = NULL;
// 1 ~ N까지의 숫자를 모두 저장하는 트립 생성
for (int i = 0; i < N; i++)
candidate = insert(candidate, new Node(i + 1));
// 뒤에서부터 A[]를 채워나간다
for (int i = N - 1; i >= 0; i--) {
// 후보 중 이 수보다 큰 수가 larger개 있다.
int larger = shifted[i];
Node* k = kth(candidate, i + 1 - larger);
A[i] = k->key;
candidate = erase(candidate, k->key);
}
}
int main(){
cin >> C;
while (C--) {
cin >> N;
for (int i = 0; i < N; i++)
cin >> shifted[i];
// 초기 배열 형태를 구합니다.
solve();
// 초기 배열 출력
for (int i = 0; i < N; i++)
cout << A[i] << " ";
cout << endl;
}
}
'PS 문제 풀이 > Algospot' 카테고리의 다른 글
| [Algospot] 알고스팟 GRADUATION 졸업학기 (0) | 2021.03.01 |
|---|---|
| [Algospot] 알고스팟 NERD2 너드인가, 너드가 아닌가? 2 (0) | 2021.03.01 |
| [Algospot] 알고스팟 FORTRESS 요새 (0) | 2021.03.01 |
| [Algospot] 알고스팟 TRAVERSAL 트리 순회 순서 변경 (0) | 2021.03.01 |
| [Algospot] 알고스팟 ITES 외계 신호 분석 (0) | 2021.03.01 |





댓글