출처: http://www.jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=2751
Input
3
2 10
1 2 5
Output
1
로봇의 이동거리를 최소화하는 것이기 때문에 몇대의 로봇이든 움직이든 이동거리만 최소화하면 상관없습니다.
이 문제를 해결하기 위해서는 로봇의 감시 영역에 대한 구간합을 통해서 해결할 수 있습니다.

특정 지점에 두 개의 로봇이 놓일 수 없으며, 감시 영역을 최적화하기 위해 인접한 두 로봇의 감시 영역을 생각해보자.
▶ arr[i] = robot[i] - robot[i-1] - 2*R
ex) 2 - 1 - (2×2) = -3

두 영역은 『-1』 만큼 겹처서 감시를 하고 있습니다.
감시 거리 R = 2인 상태에서 최적의 구간은 아래와 같습니다.

왼쪽/오른쪽 로봇을 각각 좌우로 2만큼 이동시키는 것입니다.
(어느 한쪽만 선택해서 4만큼 이동해서도 가능하지만, 이동거리를 최소화 하는것이 목적!)
▶ 원래 위치에서는 겹치는 감시 영역이 있지만 최소한의 이동거리로 감시영역을 최적화하는 것입니다.
즉, 원래 위치에서도 두 로봇사이에서는 감시하지 못하는 영역이 없지만 좀 더 최적화 가능.
[2번째 위치와 5번째 위치 예제]

▶ 5 - 2 - (2×2) = -1
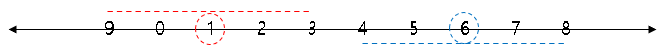
▶ 두 로봇의 최소 이동거리
abs(arr[i]) = 홀수인 경우
→ ( abs(arr[i]) + 1 ) / 2
= ( abs(robot[i] - robot[i-1] - 2*R) + 1 ) / 2
= (|-1| + 1) / 2 = 2 / 2 = 1 ← 두 로봇이 좌우로 한 칸씩 이동했다고 보면됩니다.
abs(arr[i]) = 짝수인 경우
→ abs(arr[i]) / 2
= abs(robot[i] - robot[i-1] - 2*R) / 2
지금까지 robot[] = {1, 2, 5}에서 (1, 2)와 (2, 5)를 살펴보았는데,
원형으로 이루어져 있기 때문에 마지막 로봇과 첫번째 로봇의 감시영역 고려해주어야 합니다.

즉, (5, 1)도 고려해주어야 합니다.
처음 로봇과 마지막 로봇의 감시 영역을 구할 때는 원 상의 위치 개수(=M)를 함께 고려해줍니다.
▶ arr[0] = robot[0] - robot[N - 1] - (2*R) + M ← 해당 값을 arr[0]으로 처리
→ 1 - 5 - (2×2) + 10 = 2 ← 양수(>0)로 로봇들이 감시하지 못하는 영역에 해당
→ abs(arr[i]) = 짝수 → 2 / 2 = 1 → 두 로봇이 간격을 좁혀서 감시합니다.

문제에서는 로봇이 모든 영역을 감시할 수 있게 로봇의 개수와 감시거리가 주어지므로
인접한 두 로봇의 감시 영역에서 연속구간합의 최대값을 찾으면 됩니다.
▶ robot[] 배열을 이용해서 arr[] 배열을 구한 후 (연속된 구간의 최대합 + 1) / 2 해주면 됩니다.
ex) robot[3] = {1, 2, 5} → arr[3] = {2, -3, -1}
* arr[]도 마찬가지로 원형(Circular) 수열로 놓여져 있습니다.
예를 들어 5개로 이루어진 원형수열 = {1, 2, 3, -4, 5}가 주어질 때,
→ 5, 1, 2, 3 구간의 합이 『11』 로 가장 크다.
원형 수열에서 연속구간 최대합
구간합의 최대값이 나올 수 있는 부분은 2가지 입니다.
① 중간 부분의 연속된 합 (DP로 빠르게 구할 수 있음)
② 끝 지점과 시작 시점이 포함되는 영역

즉, 직선에서의 연속구간 최대합은 ①만 고려해주면 되지만
원형이기 때문에 ②도 고려해주어야 합니다.
▶ ①과 ② 중 더 큰 값이 원형구간에서 최대값이 됩니다.
Q. 시작과 끝이 포함되는 영역에서 최대값은 어떻게 구할까?
▶ 전체합 - 연속 부분의 최소합

먼저, 중간영역에서 연속 구간 최대합을 구했듯이
기존 원소의 부호를 반대로해서 최대합을 구하면 됩니다.
→ msum (음수로서 절대값이 가장 큰 부분의 합)
그 후, 전체 합 total에서 msum 부분을 제거합니다.
→ total - msum
* 단, 예외 케이스는 모두 원소가 음수인 경우입니다.
ex) arr = [-1, -2, -3]은 전체 합(total) = -6
중간 부분에서 음수로서 절대값이 가장 큰 영역의 합(msum) = -6
결국, -6 - (-6) = 0이 되기 때문에 이러한 경우는 제외해야 합니다.
실제 연속구간 최대합 = -1
※ 관련 문제: [Jungol] 3263 연속구간최대합(Circular)
[Jungol] 정올 3263 연속구간최대합(Circular)
출처: http://jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=2556&sca=50&page=22 Input 10 4 5 -10 3 4 -7 -2 8 -6 -1 Output 10 * 대부분의 원형 문제는 직선으로 바꾸어 해결할 수 있다. 직선 구간에..
zoosso.tistory.com
실제 Input Data에서는 로봇의 위치가 무작위로 주어지므로 오름차순 정렬 → Merge Sort
#include <cstdio>
using namespace std;
const int LM = 1000000;
typedef long long LL;
int N, M, R;
LL answer, sum, msum, total;
LL min = (LL)9e9, max = -(LL)9e9;
int robot[LM], copyRobot[LM], arr[LM];
void mergeSort(int robot[], int low, int high) {
// 0. base condition
if (low >= high)
return;
// 1. divide
int mid = (low + high) / 2;
// 2. conquer
mergeSort(robot, low, mid);
mergeSort(robot, mid + 1, high);
// 3. merge
int i = low, j = mid + 1, k = low;
while (i <= mid && j <= high) {
if (robot[i] < robot[j])
copyRobot[k++] = robot[i++];
else
copyRobot[k++] = robot[j++];
}
while (i <= mid) copyRobot[k++] = robot[i++];
while (j <= high) copyRobot[k++] = robot[j++];
// 4. copy
for (i = low; i <= high; ++i)
robot[i] = copyRobot[i];
}
int main(void) {
scanf("%d %d %d", &N, &R, &M);
for (int i = 0; i < N; i++)
scanf("%d", robot + i);
// 로봇 오름차순 정렬
mergeSort(robot, 0, N - 1);
// 첫번째 위치의 로봇과 마지막 위치의 로봇의 감시 범위
arr[0] = robot[0] - robot[N - 1] - (2*R) + M;
for (int i = 0; i < N; i++) {
if (i >= 1)
arr[i] = robot[i] - robot[i - 1] - 2 * R;
// arr[] 전체 원소의 합
total += arr[i];
// 중간 영역에서 연속구간 합의 최대값
if (sum > 0) sum += arr[i];
else sum = arr[i];
max = max < sum ? sum : max;
// 중간 영역에서 연속구간 합의 최소값
if (msum < 0) msum += arr[i];
else msum = arr[i];
min = min > msum ? msum : min;
}
// 원형 수열에서 연속구간 합의 최대값
answer = max > (total - min) ? max : (total - min);
// 로봇들이 움직일 필요없이 이미 모든 영역을 감시하는 경우
if (answer <= 0)
answer = 0;
else // (소수점은 버려지므로) 홀수, 짝수 구분하지 않고 처리
answer = (answer + 1) / 2;
printf("%lld\n", answer);
}
'PS 문제 풀이 > Jungol' 카테고리의 다른 글
| [Jungol] 정올 1156 책 복사하기2 (0) | 2021.03.02 |
|---|---|
| [Jungol] 정올 2306 두 용액 (0) | 2021.02.28 |
| [Jungol] 정올 3263 연속구간최대합(Circular) (0) | 2021.02.28 |
| [Jungol] 정올 1836 연속부분합 찾기 (0) | 2021.02.28 |
| [Jungol] 정올 2497 수열 (0) | 2021.02.28 |





댓글