출처: jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=3055&sca=99&page=24
Input
4
5 -5 -7 7
Output
3
[해시] Hash란?
Hash란? 원소가 저장되는 위치가 원소 값에 의해 결정되는 자료구조 - 평균 상수 시간에 삽입, 검색, 삭제가 가능하다. - 매우 빠른 응답을 요구하는 상황에 유용 (Hash는 최소(최대) 원소를 찾는 것
zoosso.tistory.com
연속구간의 합을 구해야 한다는 점에서 prefix sum을 이용하면 좋을 것 같다는 생각이 듭니다.
간단하게 생각했을 때는 psum = 0인 개수만 찾으면 되지 않을까 생각할 수 있지만,
psum = 0이 아니어도 문제에서 요구한 구간의 합 = 0이 될 수 있습니다.
ex) arr = [1 5 -5 7 -7]
psum = [1 6 1 8 -1] ← psum[i] = 0은 없지만
(5, -5), (7, -7), (5, -5, 7, -7) 3개 모두 구간합 = 0이 될 수 있습니다.
이 문제는 pusm[]에서 아래의 규칙을 찾아내면 해결할 수 있습니다.

Q. 구간 합 = 0이 되는 지점은 어디일까?
[2, 3] = -2 + 2 = 0
[4, 7] = -2 -1 -1 + 4 = 0
[2, 7] = -2 + 2 - 2 - 1 - 1 + 4 = 0
▶ psum[i] = 3이 처음 나오고 다시 등장할 때, 구간합 = 0이 되는 특징을 찾을 수 있습니다.

if) A[] 크기를 더 확장하여 psum[i] = 3인 경우가 한번 더 있다고 가정하면 3개 더해져 총 6가지가 되고
또 한번 더 있다고 가정하면, 4개가 늘어나 10가지가 될 것입니다.
* 0은 단독으로 구간합 = 0이 될 수 있습니다.
(psum = 0은 혼자서도 연속 부분합을 0을 만들기에
최초의 psum[i] = 0도 개수에 포함시켜야 합니다.)
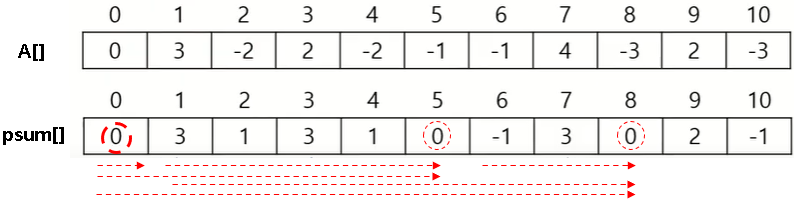
위의 경우에는 psum[i] = 0으로서 구간합 = 0이 되는 구간은 6가지 입니다.
▶ psum[i] = 음수여도 상관이 없습니다.

[7, 10] = 4 -3 + 2 - 3 = 0
▶ psum[i]가 등장하는 횟수를 저장하는 cnt[]을 만듭니다.
0은 혼자서도 연속 부분합을 만들기에 cnt[0] = 1로 초기화하고 나머지는 cnt[i] = 0으로 초기화
prefix sum을 구하는 과정에서 매 시점 sum에 대하여 ans += cnt[idx];과 cnt[idx]++; 처리
위의 규칙과 함께 이 문제는 메모리를 신경써주어야 합니다. (64MB 제한)
Input Data 범위: 원소의 개수 (1 ≤ n ≤ 100,000)이며 각 원소는 (-100 ≤ ai ≤ 100)
부분합의 범위는 -1,000만 ~1,000만이기에 구간을 shift하여 0~2,000만으로 시도할 수 있습니다.
But) 64MB / 4byte (int형) = 16MB = 1,600만이기 때문에 2,000만 크기의 배열을 만들 수 없습니다.
(배열 뿐만 아니라 다른 변수를 고려한다면 다른 방법이 필요.)
unsigned short형 변수라 해도 표현 가능한 수는 0 ~ 65535까지만 가능
부분합 = 0을 만들기 위해서는 특정 구간 합이 X 라면 그것에 상응하는 값인 -X가 필요합니다.
▶ X - X = 0이 될 수 있기 때문입니다.
그렇다면 특정 구간의 합이 -600만라면 다른 구간에서 600만이 필요하지만
해당 문제에서는 n ≤ 100,000으로 가능성이 없습니다.
즉, -500만 보다 작거나 500만보다 큰 연속부분합은 0을 만들 가능성이 없는 것입니다.
ex) 구간 내 연속 부분합의 최대값이 800만이라면 구간 내 연속 부분합의 최솟값은 -200만 보다 작을 수 없습니다.
따라서 int형 배열 크기 1000만인 cnt[]을 만들어 문제를 해결할 수 있습니다.
→ 1,000만 × 4(int) / 1,048,576(1M) = 약 38MB
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
using namespace std;
const int LM = 5000000;
int N, cnt[LM * 2 + 5];
long long ans;
int main() {
// freopen("sample_input.txt", "r", stdin);
int i, num, sum = 0, idx;
cnt[LM] = 1; //실제값은 0, 0을 shift 500만
scanf("%d", &N);
for (i = 0; i < N; i++){
scanf("%d", &num);
sum += num;
// -5백만~5백만 사이만 고려
if (-LM <= sum && sum <= LM) {
idx = sum + LM;
ans += cnt[idx];
cnt[idx]++;
}
}
printf("%lld\n", ans);
}
구간합의 최소값 minSum의 초기값을 0으로 합니다.
연속된 구간합의 최솟값 minSum을 구하고 ADD = -minSum으로 한 후,
ADD만큼 구간 Shift하여 처리합니다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
const int LM = 100010;
int minSum, sum, ADD;
int N, psum[LM], cnt[LM * 100];
long long ans;
int main() {
// freopen("input.txt", "r", stdin);
scanf("%d", &N);
int i, num;
for (i = 1; i <= N; i++) {
scanf("%d", &num);
psum[i] = psum[i - 1] + num;
if (sum < 0) sum += num;
else sum = num;
if (minSum > sum) minSum = sum;
}
ADD = -minSum;
cnt[ADD] = 1;
for (i = 1; i <= N; ++i) {
int idx = psum[i] + ADD;
ans += cnt[idx];
cnt[idx]++;
}
printf("%lld\n", ans);
}
'PS 문제 풀이 > Jungol' 카테고리의 다른 글
| [Jungol] 정올 1836 연속부분합 찾기 (0) | 2021.02.28 |
|---|---|
| [Jungol] 정올 2497 수열 (0) | 2021.02.28 |
| [Jungol] 정올 3136 const 구간의 합 구하기(2D) (0) | 2021.02.28 |
| [Jungol] 정올 1437 같은 모양 찾기 (0) | 2021.02.28 |
| [Jungol] 정올 2097 지하철 (0) | 2021.02.27 |





댓글