출처: http://www.jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=681&sca=4030
Input
2
Output
3
1 : A->B
2 : A->D
1 : B->D
▶ hanoi4(n, 1, 2, 3, 4)
: 1번 기둥에 있는 n개의 원판을 4번 기둥으로 이동시키는데 2, 3번을 여분의 기둥으로 이용
hanoi4(n, 1, 2, 3, 4)에서 n개의 원판 중 일부인 K개를 2번 기둥에 이동시키는 것을
hanoi4(k, 1, 3, 4, 2)라고 할 수 있습니다.
(여분의 기둥을 한 개 활용하고자 하는 것이기 때문에 3번 기둥으로 이동한다고 생각해도 상관 X)
(이때, K는 임의의 수가 될 수 없으면 최적화 수치가 필요합니다.)
k개를 2번 기둥에 옮겨놓았으므로 n-k개의 원판을 이동할 때는 2번 기둥을 사용하수 없게 됩니다.
따라서 hanoi3(n-k, 1, 3, 4)가 되고 [Jungol] 1161 하노이 1(3기둥) 와 유사하게 됩니다.
[Jungol] 정올 1161 하노이1
출처: http://www.jungol.co.kr/bbs/board.php?bo_table=pbank&wr_id=441&sca=2070 Input 3 Output 1 : 1 -> 3 2 : 1 -> 2 1 : 3 -> 2 3 : 1 -> 3 1 : 2 -> 1 2 : 2 -> 3 1 : 1 -> 3 ▶ hanoi(원판 수, 시작..
zoosso.tistory.com
이제 2번 기둥에 있는 k개의 원판을 hanoi4(k, 2, 1, 3, 4)하여 이동 끝
즉, k개 여분의 기둥 중 한 곳으로 옮겨놓아서 n-k개에 대해 기둥 3개인 문제로 접근합니다.
- hanoi3(): 기둥이 3개 있을 때 최소 이동 횟수
- hanoi4(): 기둥이 4개 있을 때 최소 이동 횟수
void hanoi4(int n, int a, int b, int c, int d) {
if (n == 0) return;
hanoi4(k, a, c, d, b); // k개 원판을 여분의 기둥 b에 옮기고
hanoi3(n - k, n, a, c, d); // 남은 n-k 원판을 목적지로 옮긴다.
hanoi4(k, b, a, c, d); // b에 있는 k개의 원판을 d로 옮긴다.
}
결국, k가 어떤 수치여야 hanoi4가 최소가 될 수 있는지 생각해야 합니다. (1 ≤ K < N)
- 기둥이 3개인 경우: H3[n] = 2n-1 ← 수학적으로 증명된 수치
- 기둥이 4개인 경우: H4[n] = H4[k] * 2 + H3[n-k] 수식에서
k를 1부터 n-1까지 넣어보면서 결과가 최소가 되는 k를 찾아야 합니다.
수식 도출 과정

Q. 최적의 k는 어떻게 찾아낼까?
moveK[n] = k = H4[n]을 최소 이동횟수로 하는 k
초기값 H3[1] = 1, H4[1] = 1 ← 원판이 1개일 때 최소 이동수는 1개입니다.
moveK[1] = 0 ← 원판이 1개 일 때, 여분의 기둥을 사용하지 않습니다.
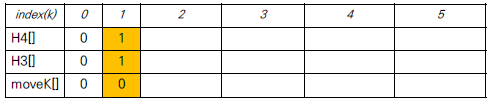
- H3[2] = 22-1 = 3
- H4[2] = H4[1] * 2 + H3[2-1] (1 ≤ k < 2)
→ H4[n]을 최적으로 하는 k = 1 = moveK[2]

* 표와 도형은 moveK[]의 규칙을 파악하기 위함.
- H3[3] = 23-1 = 7
- H4[3] = H4[1] * 2 + H3[3-1] (1 ≤ k < 3)
→ H4[n]을 최적으로 하는 k는 1, 2 중에서 1(= moveK[3]) 입니다.

- H3[4] = 24-1 = 15
- H4[4] = H4[2] * 2 + H3[4-2] (1 ≤ k < 4)
→ H4[n]을 최적으로 하는 k는 1, 2, 3 중에서 2(= moveK[4]) 입니다.

- H3[5] = 25-1 = 31
- H4[5] = H4[2] * 2 + H3[5-2] (1 ≤ k < 5)
→ H4[n]을 최적으로 하는 k는 1, 2, 3, 4 중에서 2(= moveK[5]) 입니다.

▶ moveK를 DP로 구할 수 있습니다.
int h4[22] = {0, 1}, moveK[22];
void moveCnt(){
int i, j;
for(i=2; i<=N; ++i){
h4[i] = (1<<i) - 1;
for(j=1; j<i; ++j){
int t = h4[j] * 2 + (1<<(i-j)) -1;
if(t < h4[i]){
h4[i] = t;
moveK[i] = j;
}
}
}
}#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int N;
int moveK[22];
// N은 최대 20이므로 재귀함수(recursive)로 구현
int moveCnt(int n) {
if (n < 2) return n;
int ret = (1 << n) - 1;
for (int k = 1; k < n; ++k) {
int t = moveCnt(k) * 2 + ((1 << (n - k)) - 1);
if (t < ret) {
ret = t;
moveK[n] = k;
}
}
return ret;
}
void hanoi3(int n, int num, int a, int b, int c) {
if (n == 0) return;
hanoi3(n - 1, num - 1, a, c, b);
printf("%d : %c->%c\n", num, a + 64, c + 64);
hanoi3(n - 1, num - 1, b, a, c);
}
void hanoi4(int n, int a, int b, int c, int d) {
if (n == 0) return;
hanoi4(moveK[n], a, c, d, b);
hanoi3(n - moveK[n], n, a, c, d);
hanoi4(moveK[n], b, a, c, d);
}
int main() {
scanf("%d", &N);
int ans = moveCnt(N);
printf("%d\n", ans);
hanoi4(N, 1, 2, 3, 4);
return 0;
}
'PS 문제 풀이 > Jungol' 카테고리의 다른 글
| [Jungol] 정올 1570 중앙값 (0) | 2021.02.27 |
|---|---|
| [Jungol] 정올 2082 힙정렬2 (Heap_Sort) (0) | 2021.02.27 |
| [Jungol] 정올 1912 미로탐색 (0) | 2021.02.27 |
| [Jungol] 정올 1824 스도쿠 (0) | 2021.02.27 |
| [Jungol] 정올 1161 하노이1 (0) | 2021.02.27 |




댓글