반응형
출처: https://www.acmicpc.net/problem/11657
Input
3 4
1 2 4
1 3 3
2 3 -1
3 1 -2
Output
4
3
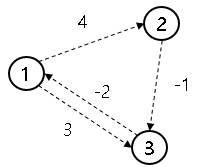
음수 가중치를 포함하는 유향 그래프에서 최단 거리를 구하는 문제이므로
벨만-포드 (Bellman-Ford)
개념 가중 유향 그래프에서 최단 경로를 구하는 알고리즘입니다. 벨만 포드 알고리즘은 동작원리는 다익스트라(Dijkstra)와 유사합니다. 차이점은 벨만 포드는 음수 가중치가 존재하는 경우에도
zoosso.tistory.com
▷ 음수 사이클을 형성하는 경우
Input
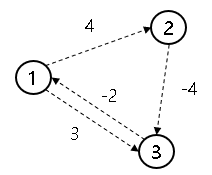
3 4
1 2 4
1 3 3
2 3 -4
3 1 -2
Output
-1
Input
3 2
1 2 4
1 2 3
Output
3
-1
▷ [1] → [3]로 가는 경로가 존재 X

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static final int INF = 1000000000;
static int N, M, K;
static int[] dist; // 최소 거리 비용 테이블
static Edge[] edge;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = null;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); // 정점의 개수
M = Integer.parseInt(st.nextToken()); // 간선의 개수
// dist[] INF로 초기화
dist = new int[N + 1];
Arrays.fill(dist, INF);
// 출발정점
dist[1] = 0;
// 간선 정보
edge = new Edge[M];
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
edge[i] = new Edge(from, to, cost);
}
// 벨먼 포드 알고리즘 결과에 따른 처리
printAnswer(bellmanFord());
}
private static boolean bellmanFord() {
// 최단 경로를 가질 수 있는 최대 크기(|V[G]|-1)만큼 반복
for (int i = 1; i <= N - 1; i++) {
// 모든 간선(edge)에 대해서 순회
for (int j = 0; j < M; j++) {
// 해당 정점이 아직 연결된 단계가 아니라면 continue
if (dist[edge[j].from] >= INF)
continue;
// Relaxation
if (dist[edge[j].to] > dist[edge[j].from] + edge[j].cost) {
dist[edge[j].to] = dist[edge[j].from] + edge[j].cost;
}
}
}
// Negative edge cost cycles 여부 확인
// 이전 단계에서 for문을 |V[G]|-1 완료한 상태에서 한번 더 최단 거리 비용 갱신 시도
for (int i = 0; i < M; i++) {
// 연결되어 있지 않은 지점은 continue
if (dist[edge[i].from] >= INF)
continue;
// 최단 거리 비용이 갱신되는 곳이 있다면 음수 사이클을 형성하고 있음.
if (dist[edge[i].to] > dist[edge[i].from] + edge[i].cost) {
return false;
}
}
return true;
}
public static void printAnswer(boolean isPossible) {
StringBuilder sb = new StringBuilder();
if (isPossible) {
// 출발 정점을 제외하고 최소 거리 비용 출력
for (int i = 2; i <= N; i++) {
// 연결되어 있지 않아 도달할 수 없다면 -1
sb.append(dist[i] == INF ? -1 : dist[i]);
sb.append("\n");
}
} else {
sb.append("-1");
}
System.out.println(sb.toString());
}
}
class Edge {
int from, to;
int cost;
public Edge(int from, int to, int cost) {
this.from = from;
this.to = to;
this.cost = cost;
}
}
반응형
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 9517 아이 러브 크로아티아 (0) | 2021.02.26 |
|---|---|
| [BOJ] 백준 1022 소용돌이 예쁘게 출력하기 (0) | 2021.02.26 |
| [BOJ] 백준 1927 최소 힙 (0) | 2021.02.26 |
| [BOJ] 백준 11279 최대 힙 (0) | 2021.02.26 |
| [BOJ] 백준 1748 수 이어 쓰기 1 (0) | 2021.02.26 |





댓글