출처: https://www.acmicpc.net/problem/7453
Input
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45
Output
5
▶ A + B + C + D = 0
-45 + -27 + 42 + 30 = 0
26 + 30 + -10 + -46 = 0
-32 + 22 + 56 + -46 = 0
-32 + 30 + -75 + 77 = 0
-32 + -54 + 56 + 30 = 0

[방법 1] Brute Force
▶ 4중 반복문을 구현하여 완전탐색으로 구할 수 있지만 TLE 발생
[방법 2] Radix Sort
▶ A + B + C + D = 0 → (A + B) = -(C + D)
즉, 네 정수를 더하여 0이 되는 문제를 두 수를 더하여 같은 수치(절대값)를 갖는 문제로 풀 수 있습니다.
(A[i] + B[j])의 결과와 C[i] + D[j] 결과를 각각 구한 후 정렬해서 two point 기법으로 찾을 수 있습니다.
따라서, 정렬을 어떻게 구현할 것인가를 고민해야 합니다.
이 문제의 경우, 기수 정렬을 이용하되 10진 기수 정렬은 나머지 연산의 Overhead로 TLE 발생하므로
8bit, 16bit 등의 비트 단위 기수 정렬을 이용하여 해결 가능
※ 나머지 연산(%) 보다는 비트연산으로 하는것이 더 효율적
▶ a % b = a - a / b * b
▶ x % 2k = x & (2k-1)
[방법 3] Hash
① (A[i] + B[j])를 해시테이블에 key와 개수 변수 cnt로 저장
② -(C[i] + D[j]) 결과를 key로 해서 Hash에 저장된 cnt를 얻어 냅니다.
결과적으로 Hash Table을 얼마나 효율적으로 구성할지가 중요합니다.
※ 충돌해결법으로 Chaining과 Open addressing (Linear Probing)을 구현
[해시] Hash란?
Hash란? 원소가 저장되는 위치가 원소 값에 의해 결정되는 자료구조 - 평균 상수 시간에 삽입, 검색, 삭제가 가능하다. - 매우 빠른 응답을 요구하는 상황에 유용 (Hash는 최소(최대) 원소를 찾는 것
zoosso.tistory.com
Chaning Version

▶ A[i] = -1일 때, A[i] + B[j] → {-3, -2, 3}
(-1 -2 = -3) / (-1 -1 = -2) / (-1 + 4 = 3)
▶ A[i] = -2일 때, A[i] + B[j] → {-4, -3, 2}
(-2 -2 = -4) / (-2 -1 = -3) / (-2 + 4 = 2)
▶ A[i] = -2일 때, A[i] + B[j] → {-4, -3, 2}
(-2 -2 = -4) / (-2 -1 = -3) / (-2 + 4 = 2)
C[i] + D[j] 결과와 동일한 값이 Hash에 있는지 확인하여 처리합니다.
(* Sample Case 숫자 상태에 따라 링크드 리스트로 인해 메모리가 부족할 수 있음)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
typedef unsigned int UI;
const int LM = 4000;
const int SIZE = 1048576; // 2^20
const int MOD = SIZE - 1;
int N, A[LM], B[LM], C[LM], D[LM];
long long ans;
struct Node {
UI key, cnt;
Node* next;
Node* alloc(UI nk, Node* np) {
key = nk, cnt = 1, next = np;
return this;
}
}buf[LM * LM + 5], * htab[SIZE];
int bcnt;
Node* probing(UI key, int hIdx) {
Node* p = htab[hIdx];
for (; p; p = p->next) {
if (p->key == key) return p;
}
return NULL;
}
int main() {
// freopen("input.txt", "r", stdin);
register int i, j;
scanf("%d", &N);
for (i = 0; i < N; ++i) {
scanf("%d%d%d%d", A + i, B + i, C + i, D + i);
}
// A[] + B[] process
for (i = 0; i < N; ++i) {
for (j = 0; j < N; ++j) {
UI key = A[i] + B[j];
int hidx = key & MOD; // key % SIZE 결과와 동일
Node* p = probing(key, hidx); // Hash Table에 존재하고 있는지 확인
if (p) // 존재하는 경우, 개수(cnt)를 올려준다.
p->cnt++;
else // 없는 경우, 해당 key에 새로운 value로 추가(chaining 기법)
htab[hidx] = buf[bcnt++].alloc(key, htab[hidx]);
}
}
// C[] + D[] process
for (i = 0; i < N; ++i) {
for (j = 0; j < N; ++j) {
UI key = -(C[i] + D[j]);
int hidx = key & MOD; // key % SIZE
Node* p = probing(key, hidx);
// 같은 수치가 존재하는 경우만 ans에 누적
if (p) ans += p->cnt;
}
}
printf("%lld\n", ans);
}
Open Addressing (Linear Probing)
- SIZE에 따라 적재율(Load Factor)이 달라지면서 동시에 시간복잡도가 달라짐
- Chaining 기법보다 추가 메모리를 잡지 않는 장점이 있음
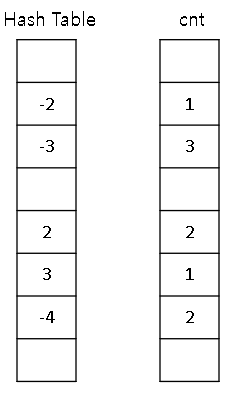
- A[i] + B[j] 결과 값을 저장하는 Hash Table과 해당 결과가 몇 번 나왔는지 저장하는 cnt[] 배열 이용
결과 값을 Hash Table에 저장할 때, 충돌이 일어나는 경우 비어있는 공간을 찾는 것이 Open Addressing 기법의 주요 개념
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
typedef unsigned int UI;
const int LM = 4000;
const int SIZE = 29999999;
int N, A[LM], B[LM], C[LM], D[LM];
long long ans;
UI hTable[SIZE], cnt[SIZE];
int probing(UI key, register int hidx) {
for (; ; hidx = (hidx + 1) % SIZE) {
if (cnt[hidx] && hTable[hidx] == key)
// cnt[] > 0으로, Hash Table에서 이미 배정된 key 값인 경우
return hidx;
else if (cnt[hidx] == 0)
// cnt[]가 비어있는 곳(=0)으로, Hash Table에서도 key값이 비어있는 위치를 반환
return hidx;
}
return hidx;
}
int main() {
// freopen("input.txt", "r", stdin);
register int i, j;
scanf("%d", &N);
for (i = 0; i < N; ++i) {
scanf("%d%d%d%d", A + i, B + i, C + i, D + i);
}
// A[] + B[] process
for (i = 0; i < N; ++i) {
for (j = 0; j < N; ++j) {
UI key = A[i] + B[j];
int hidx = probing(key, key % SIZE);
// cnt[]가 비어있는 곳(=0)으로, Hash Table에서도 key값이 비어있는 곳에 배정
if (cnt[hidx] == 0)
hTable[hidx] = key;
cnt[hidx]++;
}
}
// C[] + D[] process
for (i = 0; i < N; ++i) {
for (j = 0; j < N; ++j) {
UI key = -(C[i] + D[j]);
int hidx = probing(key, key % SIZE);
ans += cnt[hidx];
}
}
printf("%lld\n", ans);
}
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 1406 에디터 (0) | 2021.02.25 |
|---|---|
| [BOJ] 백준 3033 가장 긴 문자열 (0) | 2021.02.25 |
| [BOJ] 백준 17619 개구리 점프 (0) | 2021.02.25 |
| [BOJ] 백준 17615 볼 모으기 (0) | 2021.02.25 |
| [BOJ] 백준 2450 모양 정돈 (0) | 2021.02.25 |





댓글