반응형
정점 u - v 간 간선 여부 확인
- 인접 리스트는 adList[u]의 처음부터 읽어나가면서 각 원소를 일일이 확인
- 인접 행렬은은 정점 u, v가 주어졌을 때, 단 한 번의 배열의 접근으로 연결 여부 확인
공간 복잡도
- 인접행렬: V × V 개수 만큼 공간 필요
- 인접리스트: 정점 개수 V와 실제 간선의 개수 E에 좌우 (V + E)
(만약 간선의 개수가 V에 수렵한다면 인접행렬 비슷한 공간복잡도를 가짐)
결론
- 간선의 수가 V2에 비해 훨씬 적은 그래프를 희소 그래프 → 인접 리스트
- 간선의 수가 V2에 비례하는 그래프를 밀접 그래프 → 인접 행렬
방향성 그래프 (인접 리스트)
import java.util.ArrayList;
import java.util.Iterator;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// vertex의 개수
int vCnt = Integer.parseInt(sc.next());
// edge의 개수
int eCnt = Integer.parseInt(sc.next());
ArrayList<ArrayList<Integer>> adList = new ArrayList<>();
// 리스트 인덱스 '1'로 하기에 dummy data로 한 개 넣어둠
adList.add(new<Integer> ArrayList());
for(int i=0; i<vCnt; i++) {
adList.add(new<Integer> ArrayList());
}
for(int i=0;i<eCnt;i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adList.get(v1).add(v2);
}
//인접리스트 출력
for(int i=1; i<=vCnt; i++) {
Iterator<Integer> iter = adList.get(i).iterator();
System.out.print("[" + i + "]: ");
while(iter.hasNext()) {
System.out.print(iter.next() + " ");
}
System.out.println();
}
}
}
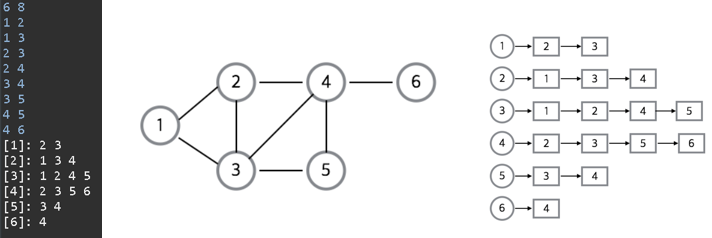
비방향성 그래프 (인접 리스트)
import java.util.ArrayList;
import java.util.Iterator;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// vertex의 개수
int vCnt = Integer.parseInt(sc.next());
// edge의 개수
int eCnt = Integer.parseInt(sc.next());
ArrayList<ArrayList<Integer>> adList = new ArrayList<>();
// 리스트 인덱스 '1'로 하기에 dummy data로 한 개 넣어둠
adList.add(new<Integer> ArrayList());
for(int i=0; i<vCnt; i++) {
adList.add(new<Integer> ArrayList());
}
for(int i=0;i<eCnt;i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
// 비방향 그래프이기 때문에 양쪽에 edge가 있다는것을 구현해야 한다.
adList.get(v1).add(v2);
adList.get(v2).add(v1);
}
//인접리스트 출력
for(int i=1; i<=vCnt; i++) {
Iterator<Integer> iter = adList.get(i).iterator();
System.out.print("[" + i + "]: ");
while(iter.hasNext()) {
System.out.print(iter.next() + " ");
}
System.out.println();
}
}
}
방향성 그래프 (인접 행렬)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// vertex의 개수
int vCnt = Integer.parseInt(sc.next());
// edge의 개수
int eCnt = Integer.parseInt(sc.next());
// 리스트 인덱스 '1'로 하기에 크기를 1개 늘려서 할당
int[][] adMatrix = new int[vCnt+1][vCnt+1];
for(int i=0;i<eCnt;i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adMatrix[v1][v2] = 1;
}
for(int i=1; i<=vCnt; i++) {
System.out.print("[" + i + "]: ");
for(int j=1; j<=vCnt; j++) {
System.out.print(adMatrix[i][j]+ " ");
}
System.out.println();
}
}
}
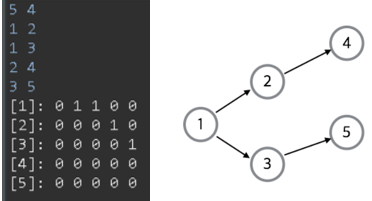
비방향성 그래프 (인접 행렬)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// vertex의 개수
int vCnt = Integer.parseInt(sc.next());
// edge의 개수
int eCnt = Integer.parseInt(sc.next());
// 리스트 인덱스 '1'로 하기에 크기를 1개 늘려서 할당
int[][] adMatrix = new int[vCnt+1][vCnt+1];
for(int i=0;i<eCnt;i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adMatrix[v1][v2] = 1;
adMatrix[v2][v1] = 1;
}
for(int i=1; i<=vCnt; i++) {
for(int j=1; j<=vCnt; j++) {
System.out.print(adMatrix[j][i]+ " ");
}
System.out.println();
}
}
}

반응형
'자료구조' 카테고리의 다른 글
| [스택] Stack 이란? (0) | 2021.04.22 |
|---|---|
| 우선순위 큐 (Priority Queue) (0) | 2021.03.21 |
| 힙(Heap) 시뮬레이션 (0) | 2021.02.27 |
| 힙(Heap) 자료구조란? (0) | 2021.02.27 |
| 그래프 정의 및 구현 방식 (인접 행렬 & 인접 리스트) (0) | 2021.02.25 |





댓글