개념
아래와 같은 가중 그래프에서 최단 경로를 찾는 알고리즘.

ex) 정점 ③ → ⑤로 가는 최단 경로는 다음과 같습니다.
경로Path: ③ → ② → ④ → ① → ⑤
비용Cost: +4 +1 +2 -4 = 3
플로이드 와샬을 이용해서 정점 [u] → 정점 [v]로 가는 최단 거리를 구할 때,
아래의 두 개의 테이블을 이용합니다.
- 최단 거리 비용을 나타내는 테이블 D
- 최단 거리 경로를 구할 수 있는 테이블 P
시뮬레이션
▶ 초기 테이블 상태

- (테이블 D) 『INF』: 현재 시점에서 바로 연결되어 있지 않기에 무한대.
- (테이블 P) 『NIL』: 경로가 없다.
▶ 중간 경로로 정점 [1] 추가

정점 [1]을 중간 경유하여 최단 거리 비용 테이블 D가 갱신됩니다.
· [4] → [1] → [2] ▷ D[4][1] + D[1][2] = 2 + 3
▶ 『 INF 』 → 『 5 』
· [4] → [1] → [5] ▷ D[4][1] + D[1][2] = 2 + (-4)
▶ 『 INF 』 → 『 -2 』
※ [P 테이블] P[4][2] = P[4][5] = 1이므로 변화가 없습니다.
▶ 중간 경로로 정점 [2] 추가

· [1] → [2] → [4] ▷ D[1][2] + D[2][4] = 3 + 1
▶ 『 INF 』 → 『 4 』
· [3] → [2] → [4] ▷ D[3][2] + D[2][4] = 4 + 1
▶ 『 INF 』 → 『 5 』
· [3] → [2] → [5] ▷ D[3][2] + D[2][5] = 4 + 7
▶ 『 INF 』 → 『 11 』
※ [P 테이블] P[1][4] = P[3][4] = P[3][5] 값을 중간정점 [2]로 갱신
▶ 중간 경로로 정점 [3] 추가

정점 [3]을 중간 경유하여 기존의 [4] → [2] 최단거리가 기존값에서 갱신됩니다.
path: [4] → [1] → [2] ▶ [4] → [3] → [2]
cost: 『 5 』 ▶ (-5) + (4) ▶ 『 -1 』
▶ 중간 경로로 정점 [4] 추가

▶ 중간 경로로 정점 [5] 추가

ex) 정점 [5]을 중간 경유하여 기존의 [1] → [3] 최단거리가 갱신됩니다.
path: [1] → [2] → [4] → [3] ▶ [1] → [5] → [4] → [3]
cost: 『 -1 』 ▶ 『 -3 』
완성된 테이블 해석

[테이블 D]에서 u → v로 가는 최단 거리 비용을 알 수 있습니다.
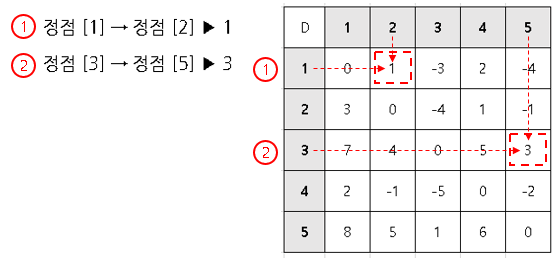
[테이블 P]에서 u → v로 가는 최단 거리 경로를 알 수 있습니다.
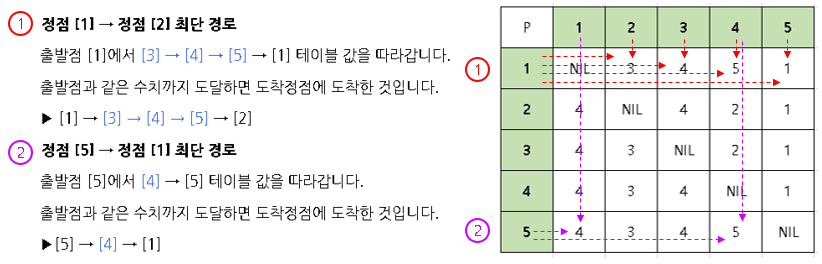
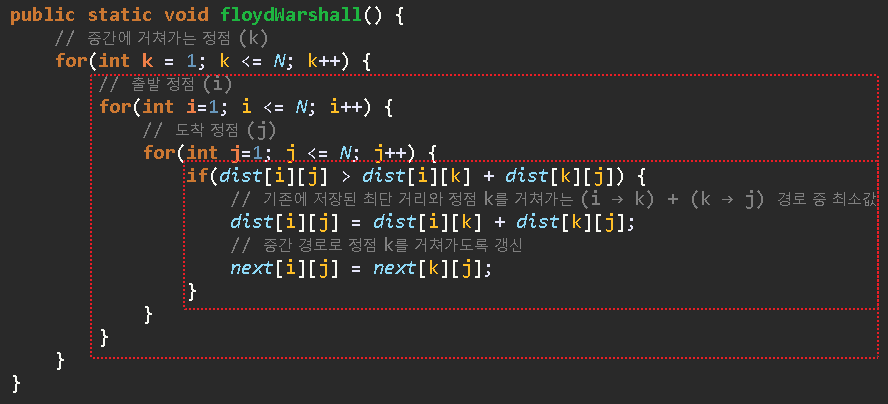
구현
- 테이블을 초기화한 후, 삼중 for문을 통해 구현 시간 복잡도 = O( |V|3 )
- u → v로 가는 최단 거리 비용 테이블을 중간 정점 [k] 추가하며 갱신
관련 문제
★ [BOJ] 11404 플로이드 (최단 거리 비용)
★ [BOJ] 11780 플로이드 2 (최단 거리 비용 + 경로)
- [SWEA] 4066 All Pair Shortest Path

'알고리즘' 카테고리의 다른 글
| 벨만-포드 (Bellman-Ford) (0) | 2021.02.26 |
|---|---|
| 다익스트라 (Dijkstra) (0) | 2021.02.25 |
| 위상정렬 (Topological sort) (0) | 2021.02.24 |
| 버블 정렬(Bubble Sort) (0) | 2021.02.24 |
| DFS와 BFS 비교 (0) | 2021.02.24 |





댓글