출처: www.acmicpc.net/problem/2056
Input
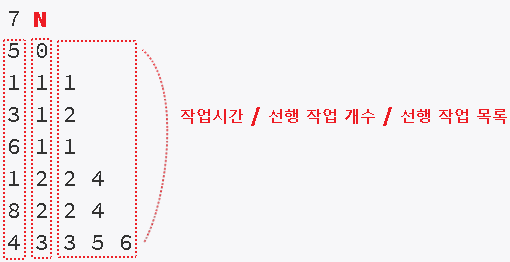
7
5 0
1 1 1
3 1 2
6 1 1
1 2 2 4
8 2 2 4
4 3 3 5 6
Output
23
위상정렬 (Topological sort)
개념 DAG에서 의존성에 맞게 그래프의 정점을 정렬 DAG (Directed Acyclic graph) 간선에 방향이 존재하고, 사이클(cycle)이 없는 그래프. DAG는 노드간의 의존성을 나타내는데, 작업 간의 순서를 표현하는
zoosso.tistory.com
작업(정점)의 개수 N과 각 작업별 선행관계가 주어질 때,
모든 작업이 완료하기 까지 필요한 최소 시간 출력.
1번의 경우에는 항상 선행 작업이 존재하지 않습니다.
※ 해당 문제는 사이클 유무 확인 불필요.
※ 위상정렬 순서가 아닌 작업 완료 시간을 요구하며,
선행 관계가 없는 작업들은 동시에 수행 가능
구현
그래프를 인접리스트로 표현
진입차수 위상정렬 이용.
시뮬레이션

indegree = [0 1 1 1 2 2 3]
cost = [5 0 0 0 0 0 0]

▶ 진입차수가 0인 정점 ①과 연결된 간선 처리
indegree = [0 0 1 0 2 2 3]
cost = [5 6 0 11 0 0 0]
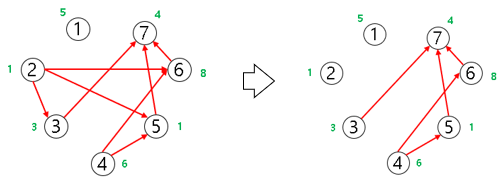
▶ 진입차수가 0인 정점 ②과 연결된 간선 처리
indegree = [0 0 0 0 1 1 3]
cost = [5 6 9 11 7 14 0]

▶ 진입차수가 0인 정점 ④와 연결된 간선 처리
indegree = [0 0 0 0 0 0 3]
cost = [5 6 9 11 12 19 0]
- 정점 ⑤의 경우 max(7, 11 + 1) = 12
- 정점 ⑥의 경우 max(14, 11 + 8) = 19
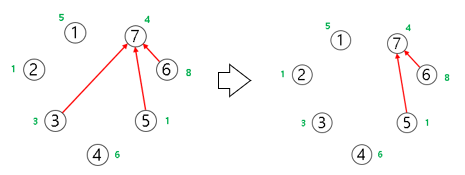
▶ 진입차수가 0인 정점 ③과 연결된 간선 처리
indegree = [0 0 0 0 0 0 2]
cost = [5 6 9 11 12 19 13]
- 정점 ⑦의 경우 max(0, 9 + 4) = 13

▶ 진입차수가 0인 정점 ⑤와 연결된 간선 처리
indegree = [0 0 0 0 0 0 1]
cost = [5 6 9 11 12 19 16]
- 정점 ⑦의 경우 max(13, 12 + 4) = 16

▶ 진입차수가 0인 정점 ⑥와 연결된 간선 처리
indegree = [0 0 0 0 0 0 0]
cost = [5 6 9 11 12 19 23]
- 정점 ⑦의 경우 max(16, 19 + 4) = 23
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static int N;
static int[] indegree, workingTime, cost;
static ArrayList<ArrayList<Integer>> adList;
static Queue<Integer> queue;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = Integer.parseInt(sc.next());
// 그래프를 인접 리스트로 표현
adList = new ArrayList<>();
adList.add(new ArrayList<>());
for(int i=0; i<N; i++) {
adList.add(new ArrayList<>());
}
// 작업시간
workingTime = new int[N+1];
// 진입차수
indegree = new int[N+1];
// 건물간의 우선순위를 생각한 비용들
cost = new int[N+1];
// 작업시간과 정점간 간선을 연결(우선 작업이 무엇인지)
for(int i=1; i<=N; i++) {
workingTime[i] = Integer.parseInt(sc.next());
int edgeCnt = Integer.parseInt(sc.next());
while(edgeCnt-- > 0) {
int head = Integer.parseInt(sc.next());
adList.get(head).add(i);
// 진입 차수 개수도 같이 counting
indegree[i]++;
}
}
queue = new LinkedList<>();
topological_sort();
int answer = 0;
for(int i=1; i<=N; i++) {
answer = answer > cost[i] ? answer: cost[i];
}
System.out.println(answer);
}
private static void topological_sort() {
// 처음 선행작업이 필요없는 작업번호를 찾는다.(문제상 1번 작업만 그것에 해당된다.)
for(int i=1; i<=N; i++) {
if(indegree[i] == 0) {
cost[i] = workingTime[i];
queue.add(i);
}
}
// queue에 있는 '작업' 한개를 꺼내 연결되어 있는 작업들이 무엇인지 확인한다.
for(int i=1; i<=N; i++) {
int curNode = queue.poll();
ArrayList<Integer> curNodeList = adList.get(curNode);
while(!curNodeList.isEmpty()) {
int target = curNodeList.remove(0);
indegree[target]--;
// 문제에서 요구한 해당 작업이 완료되기 위한 최소시간을 비교하며 도출한다.
cost[target] = Math.max(cost[target], workingTime[target] + cost[curNode] );
// indegree 개수가 새롭게 '0'이 되면 queue에 넣는다.
if(indegree[target] == 0) {
queue.add(target);
}
}
}
}
}
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 2884 알람 시계 (0) | 2021.02.24 |
|---|---|
| [BOJ] 백준 3665 최종 순위 (0) | 2021.02.24 |
| [BOJ] 백준 2252 줄 세우기 (0) | 2021.02.24 |
| [BOJ] 백준 16637 괄호 추가하기 (0) | 2021.02.24 |
| [BOJ] 백준 2661 좋은수열 (0) | 2021.02.24 |





댓글