출처: https://www.acmicpc.net/problem/17471
Input
6
2 3 4 5 6 7
2 2 3
2 1 3
2 1 2
2 5 6
2 4 6
2 4 5
Output
9
다음과 같이 그래프 정보가 주어집니다.

[그래프 형태]

하나의 정점을 지역이라고 정의하고 두 개의 선거구로 나누고자합니다.
* 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 합니다.
다른 선거구에 속한 지역을 통해서 가는 경우는 해당되지 않습니다.
* 각 구역은 두 선거구 중 하나에 포함되어야 합니다.
* 선거구는 적어도 한개의 지역을 포함해야 합니다.
[가능한 방법]

[불가능한 방법]
[좌측 그림]: 같은 선거구 지역 『5』, 『6』 연결 x
[우측 그림]: 각 선거구는 적어도 1개의 지역을 포함
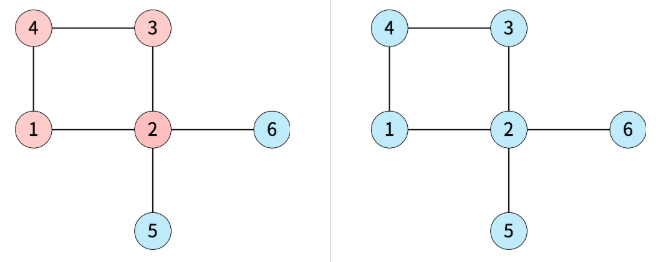
A, B 선거구가 연결되어 있거나 격리되어 있어도 상관 x
같은 선거구 내에서만 연결되어 있으면 됩니다.
선거구를 나누었을 때, 각 선거구 인구의 차이를 최소로 하려고 할 때,
인구 차이의 최솟값을 출력
Input
6
5 2 3 4 1 2
2 2 4
4 1 3 6 5
2 4 2
2 1 3
1 2
1 2
Output
1
선거구를 [1, 4] | [2, 3, 5, 6]으로 구분한 후,
각 선거구의 인구는 『9』, 『8』로 차이는 『1』
구현
① 주어진 구역을 두 개의 선거구로 나눈다. ← 조합
이때, 한 쪽의 선거구는 최소한 한 개의 지역이 존재
▶ A = {2, 3} | B = {1, 4, 5} → A에서 2개 뽑은 Case
▶ A = {1, 4, 5} | B = {2, 3} → A에서 3개 뽑은 Case
위의 경우에서 인구수를 비교할 때는 동일한 결과가 나온다.
따라서, A = {1, 2, 3, 4, 5}에서 『1 ~ N-1』개씩 뽑을 필요 없이
『1 ~ N / 2 』로 해주는 것이 효율적입니다.
② 나눠진 구역 A, B가 있으면, 해당 선거구의 구역 연결 ← 그래프, BFS
이때, 다른 선거구와 연결된 간선 이용 x
③ 위의 조건들을 만족했을 때 A, B 구역의 인구 차이가 최솟값 도출.
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;
public class Main {
static int[] people;
static int[][] graph;
static int N;
static List<Integer> A, B;
static int pickCnt;
static int answer = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = Integer.parseInt(sc.next());
// 두 선거구 A, B
A = new ArrayList<>();
B = new ArrayList<>();
// 구역별 인구 수
people = new int[N+1];
for(int i=1; i<=N; i++) {
people[i] = Integer.parseInt(sc.next());
A.add(i);
}
graph = new int[N+1][N+1];
for(int i=1; i<=N; i++) {
// 간선 개수
int cnt = Integer.parseInt(sc.next());
for(int c=0; c<cnt; c++) {
int vertex = Integer.parseInt(sc.next());
// 무방향 그래프
graph[i][vertex] = 1;
graph[vertex][i] = 1;
}
} // end of input
// A 원소 중 개 뽑아 B에 넣으면
// A 선거구에는 『(N-1)/2 ~ 1 』개가 남아 있으므로 두 선거구로 분리
int end = (N%2) == 1 ? (N/2) + 1 : (N/2);
for(pickCnt=1; pickCnt <= end; pickCnt++) {
combination(0);
}
// 두 개의 선거구로 나누는 것이 불가능했는지 확인
answer = (answer == Integer.MAX_VALUE) ? -1 : answer;
System.out.println(answer);
}
private static void combination(int idx) {
if (B.size() == pickCnt) {
// 각 선거구 연결성 확인
if(BFS(A) && BFS(B)) {
int people_of_A = 0;
for(int i=0; i<A.size(); i++) {
people_of_A += people[A.get(i)];
}
int people_of_B = 0;
for(int i=0; i<B.size(); i++) {
people_of_B += people[B.get(i)];
}
answer = Math.min(answer, Math.abs(people_of_A - people_of_B));
}
return;
}
if(idx >= A.size()) return;
// A에서 현재 idx를 뽑은 경우
B.add(A.remove(idx));
combination(idx);
A.add(idx, B.remove(B.size()-1));
// A에서 뽑지 않고 다음 인덱스로 넘어간 경우
combination(idx+1);
}
private static boolean BFS(List<Integer> list) {
Queue<Integer> queue = new LinkedList<>();
// 방문한 정점들을 저장할 배열
boolean[] visited = new boolean[graph.length+1];
// 리스트의 임의의 원소로 출발
int v = list.get(0);
queue.add(v);
// 방문한 정점 표시
visited[v] = true;
List<Integer> temp = new ArrayList<>();
while(!queue.isEmpty()) {
int cur_v = queue.poll(); // 자료구조 큐에서 Dequeue과 같은 기능
// 모두 연결되었는지 확인하기 위한 리스트
temp.add(cur_v);
// 해당 정점에서 방문할 수 있는 모든 정점 방문
for(int i=1; i<graph.length; i++) {
// 간선이 존재하고 지금까지 방문하지 않았던 정점을
if(graph[cur_v][i] == 1 && !visited[i]) {
// 소속된 선거구를 떠나서 방문표시
visited[i] = true;
// 해당 선거구의 구역인지 확인
// 같은 선거구면 BFS 탐색 지속
if(list.contains(i)) {
queue.add(i);
}
}
}
}
// 나누어진 A, B 선거구에서 빠짐없이 있는지 확인
for(int i=0; i<list.size(); i++) {
// 값을 들고 있지 않다면
if(!temp.contains(list.get(i))) {
return false;
}
}
return true;
}
}
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 11724 연결요소의 개수 (0) | 2021.02.24 |
|---|---|
| [BOJ] 백준 10026 적록색약 (0) | 2021.02.24 |
| [BOJ] 백준 1011 Fly me to the Alpha Centauri (0) | 2021.02.24 |
| [BOJ] 백준 1260 DFS와 BFS (0) | 2021.02.24 |
| [BOJ] 백준 1427 소트인사이드 (0) | 2021.02.24 |





댓글