출처: https://www.acmicpc.net/problem/2465
Input
12
120
167
163
172
145
134
182
155
167
120
119
156
0 1 0 0 3 2 6 7 4 6 9 4
Output
134
167
120
119
156
120
167
182
155
163
172
145
height[] = {120, 167, 163, 172, 145, 134, 182, 155, 167, 120, 119, 156}
S = {0 1 0 0 3 2 6 7 4 6 9 4}
→ answer[] = [134 167 120 119 156 120 167 182 155 163 172 145]
수열 S는 answer[]에서 자기보다 작은 키의 숫자입니다.
ex) 마지막 사람의 키 145cm 이하인 사람은 [134, 120, 119, 120]으로 4명입니다.
"누가 몇 번째로 작은지" 알기 위해서 먼저 키 순서대로 오름차순 정렬합니다.
정렬 후에는 뒤에서 부터 S에 해당되는 값을 찾습니다.
Q) 앞쪽부터 정할 수는 없을까?
자신보다 작은 사람 S[1] = 0 = "자신보다 작은 사람이 없다." 의미합니다.
따라서, 특정 숫자를 정할 수 없습니다.
즉, S[N] = 4로 마지막 사람(N)에서 앞쪽에 보다 작은 키가 4명 존재하는 것이기에
(정렬된 키) height[] = [119 120 120 134 145 155 156 163 167 167 172 182]에서
[119 120 120 134] 다음에 위치한 [145]가 해당됩니다.
정확히는 5번째 해당되는 숫자이며, 145는 제외됩니다.
ex) S[N-1] = 9 = 앞쪽에 보다 작은 키가 9명 존재하는 경우 = 남은 키 중에서 10번째인 사람
[119 120 120 134 145 155 156 163 167 167] 다음에 위치한 [172] (이제 172 제외)
ex) S[N-2] = 6 = 앞쪽에 보다 작은 키가 6명 존재하는 경우 = 남은 키 중에서 (6 + 1)번째인 사람
[119 120 120 134 155 156] 다음에 위치한 [163] 해당 (이제 163 제외)
▶ 이와 같이 S[N..1]까지 S[i] + 1 번째 해당하는 height[] 원소를 구간합 Segment Tree로 구합니다.
[시뮬레이션]

ex) S[N] + 1 = 5 = target에 해당하는 키 찾기
① target(=5) ≤ 6 이므로 왼쪽으로 탐색합니다.
② target(=5) > 3 이므로 오른쪽으로 탐색합니다. → target = 5 - 3 = 2
③ target(=2) ≤ 2 이므로 왼쪽으로 탐색합니다.
④ target(=2) > 1 이므로 오른쪽으로 탐색합니다.
s == e인 단말 노드이므로 tree[단말] = 145를 찾았습니다.

S[N-1] + 1 = 10 = target 키 찾기
① target(=10) > 5 이므로 오른으로 탐색합니다. → target = 10 - 5 = 5
② target(=5) > 3 이므로 오른쪽으로 탐색합니다. → target = 5 - 3 = 2
③ target(=2) ≤ 2 이므로 왼쪽으로 탐색합니다.
④ target(=2) > 1 이므로 오른쪽으로 탐색합니다.
s == e인 단말 노드이므로 tree[단말] = 172를 찾았습니다.
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
const int LM = 100000 + 10;
int N, height[LM], trr[LM];
int tree[LM * 4], S[LM], ans[LM];
void mergeSort(int start, int end) {
if (start >= end)
return;
int mid = (start + end) / 2;
mergeSort(start, mid);
mergeSort(mid + 1, end);
int i = start, j = mid + 1, k = start;
while (i <= mid && j <= end) {
if (height[i] > height[j])
trr[k++] = height[j++];
else
trr[k++] = height[i++];
}
while (i <= mid) trr[k++] = height[i++];
while (j <= end) trr[k++] = height[j++];
for (i = start; i <= end; i++) {
height[i] = trr[i];
}
}
void initTree(int n, int s, int e) {
if (s == e) {
tree[n] = 1;
return;
}
int L = n * 2, R = L + 1, mid = (s + e) / 2;
initTree(L, s, mid);
initTree(R, mid + 1, e);
tree[n] = tree[L] + tree[R];
}
// 단말 노드의 위치를 알 수 없으므로 cnt 변수를 통해서 단말 노드를 찾아갑니다.
// 탐색과정에서 제외되는 hight[] (=단말노드)가 있기 때문에 업데이터되는 구간을 직접 탐색해야 합니다.
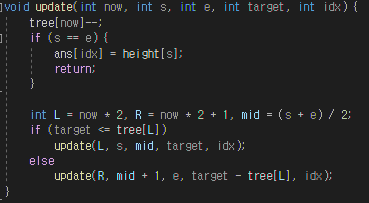
void update(int now, int s, int e, int target, int idx) {
tree[now]--;
if (s == e) {
ans[idx] = height[s];
return;
}
int L = now * 2, R = now * 2 + 1, mid = (s + e) / 2;
if (target <= tree[L])
update(L, s, mid, target, idx);
else
update(R, mid + 1, e, target - tree[L], idx);
}
int main() {
// freopen("input.txt", "r", stdin);
scanf("%d", &N);
for (int i = 1; i <= N; ++i) scanf("%d", height + i);
for (int i = 1; i <= N; ++i) scanf("%d", S + i);
mergeSort(1, N);
initTree(1, 1, N);
for (int i = N; i > 0; i--) {
update(1, 1, N, S[i] + 1, i);
}
for (int i = 1; i <= N; ++i)
printf("%d\n", ans[i]);
}
'PS 문제 풀이 > Baekjoon' 카테고리의 다른 글
| [BOJ] 백준 2487 섞기 수열 (0) | 2021.02.17 |
|---|---|
| [BOJ] 백준 7578 공장 (0) | 2021.02.17 |
| [BOJ] 백준 2630 색종이 만들기 (0) | 2021.02.17 |
| [BOJ] 백준 2479 경로 찾기 (0) | 2021.02.17 |
| [BOJ] 백준 3449 해밍 거리 (0) | 2021.02.17 |





댓글